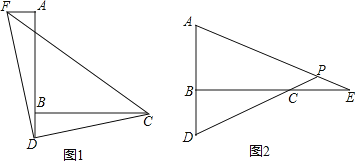
【题目】(本小题满分11分)已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
参考答案:
【答案】见解析
【解析】(1)△CDF是等腰直角三角形,(1分)
理由如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,(2分)
在△FAD与△DBC中,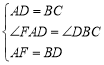 ,∴△FAD≌△DBC(SAS),(3分)
,∴△FAD≌△DBC(SAS),(3分)
∴FD=DC,∴△CDF是等腰三角形,(4分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形.(5分)
(2)作AF⊥AB于A,使AF=BD,连接DF,CF,如图,
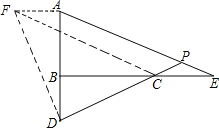
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,
在△FAD与△DBC中,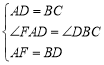 ,
,
∴△FAD≌△DBC(SAS),∴FD=DC,∴△CDF是等腰三角形,(6分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,(7分)
∴∠FCD=45°,(8分)
∵AF∥CE,且AF=CE,∴四边形AFCE是平行四边形,(10分)
∴AE∥CF,∴∠APD=∠FCD=45°.(11分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,C、D是圆O上的点,且OC∥BD,AD分别与BC、OC相交于点E、F.则下列结论:
①AD⊥BD;②∠AOC=∠ABC;③CB平分∠ABD;④AF=DF;⑤BD=2OF.
其中一定成立的是( )

A.①③⑤ B.②③④ C.②④⑤ D.①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】-2不是( ).
A.有理数
B.自然数
C.整数
D.负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年4月6日,交通运输部科学研究院对外发布《2017年第一季度中国主要城市骑行报告》,报告显示,在车均使用次数方面,昆明排名第一,成为“最爱骑共享单车的城市”.目前已经投入昆明的共享单车约有112000辆.将“112000”用科学记数法表示为( )
A.1.12×103
B.1.12×104
C.1.12×105
D.11.2×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=x2+2y2﹣z,B=﹣4x2+3y2+2z,且A+B+C=0,则多项式C为( )
A. 5x2﹣y2﹣z B. x2﹣y2﹣z C. 3x2﹣y2﹣3z D. 3x2﹣5y2﹣z
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( ).
A.非负有理数就是正有理数
B.零表示没有,是有理数
C.正整数和负整数统称为整数
D.整数和分数统称为有理数 -
科目: 来源: 题型:
查看答案和解析>>【题目】在0,1,-2,-3.5这四个数中,是负整数的是( ).
A.0
B.1
C.-2
D.-3.5
相关试题

