【题目】已知点在数轴上对应的数为，点对应的数为，关于，的多项式是6次多项式，且常数项为-6.

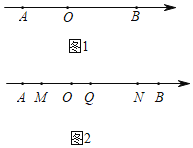
（1）点到的距离为______（直接写出结果）；

（2）如图1，点是数轴上一点，点到的距离是到的距离的3倍（即），求点在数轴上对应的数；

（3）如图2，点，分别从点，同时出发，分别以，的速度沿数轴负方向运动（在，之间，在，之间），运动时间为，点为，之间一点，且点到的距离是点到距离的一半（即），若，运动过程中到的距离（即）总为一个固定的值，求的值.

【答案】（1）8；（2）或9；（3）.

【解析】

（1）根据多项式的次数和常数项即可求解；
（2）根据两点之间的距离列等式即可求解；
（3）根据动点运动速度和时间表示线段的长，再根据Q到M的距离（即QM）总为一个固定的值与t值无关即可求解．

解：（1）根据题意，得
2a=-6，解得a=-3，b=5．
所以点A表示的数为-3，点B表示的数为5，
所以A、B之间的距离为8．
故答案为8．

（2）设点对应的数为，依题意得：

，

解得或9；

（3）依题意：，，

∴，，

∵

∴，

∴，

因为，运动过程中到的距离（即）总为一个固定的值，

即的值与无关，

即，，

∴.

关闭