【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)

参考答案:
【答案】(1)y=x2﹣4x﹣5;(2)B(5,0),C(0,﹣5);(3)![]() π.
π.
【解析】试题分析:(1)利用对称轴方程可求得b,把点A的坐标代入可求得c,可求得抛物线的解析式;(2)根据A、B关于对称轴对称可求得点B的坐标,利用抛物线的解析式可求得B点坐标;(3)根据B、C坐标可求得BC长度,由条件可知BC为过O、B、C三点的圆的直径,可求得圆的面积.
试题解析:(1)由A(﹣1,0),对称轴为x=2,可得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣4x﹣5;
(2)由A点坐标为(﹣1,0),且对称轴方程为x=2,可知AB=6,
∴OB=5,
∴B点坐标为(5,0),
∵y=x2﹣4x﹣5,
∴C点坐标为(0,﹣5);
(3)如图,连接BC,则△OBC是直角三角形,

∴过O、B、C三点的圆的直径是线段BC的长度,
在Rt△OBC中,OB=OC=5,
∴BC=5![]() ,
,
∴圆的半径为![]() ,
,
∴圆的面积为π(![]() )2=
)2=![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣2a2)2a,正确的是( )
A.2a5
B.﹣4a5
C.4a5
D.4a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】数据”1,2,1,3,1”的众数是( )
A. 1 B. 1.5 C. 1.6 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人利用不同的交通工具,沿同一路线分别从A、B两地同时出发匀速前往C地(B在A、C两地的途中).设甲、乙两车距A地的路程分别为y甲、y乙(千米),行驶的时间为x(小时),y甲、y乙与x之间的函数图象如图所示.
(1)直接写出y甲、y乙与x之间的函数表达式;
(2)如图,过点(1,0)作x轴的垂线,分别交y甲、y乙的图象于点M,N.求线段MN的长,并解释线段MN的实际意义;
(3)在乙行驶的过程中,当甲、乙两人距A地的路程差小于30千米时,求x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,对七年级1班的男生进行了100米测试,达标成绩为15秒,下表是某小组8名男生的成绩测试记录,其中“+“表示成绩大于15秒.
-0.8
+1
-1.2
0
-0.7
+0.6
-0.4
-0.1
问:(1)这个小组男生的达标率为多少?
(2)这个小组男生的平均成绩是多少秒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2+a=a3
B.a2a=a3
C.a2÷a=2
D.(2a)2=4a -
科目: 来源: 题型:
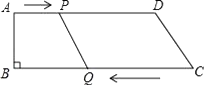
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠B﹦90°,AB﹦8cm,AD﹦24cm,BC﹦26cm,点p从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t s.
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?(等腰梯形的两腰相等,两底角相等)
相关试题

