【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);

(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
参考答案:
【答案】(1)画图见解析;(2)(2)弧AD的长为![]() π.
π.
【解析】分析: (1)作∠ABC的平分线,与AC的交点就是圆心P,此时⊙P与AB,BC两边都相切;如图,作BC的垂线PD,证明PD和半径相等即可,根据角平分线的性质可得:PA=PD.
(2)要想求劣弧AD的长,根据弧长公式需求圆心角∠APD的半径AP的长,利用四边形的内角和求∠APD=135°,再利用勾股定理和等腰三角形的性质求出AP=PD=DC=![]() 1,代入公式可求弧长.
1,代入公式可求弧长.
详解:
(1)作∠ABC的角平分线交AC于点P,以点P为圆心,AP为半径作圆.

(2)如图,∵P与AB,BC两边都相切,
∴∠BAP=∠BDP=90°,
∵∠ABC=45°,
∴∠APD=360°90°90°45°=135°,
∴∠DPC=45°,
∴△DPC是等腰直角三角形,
∴DP=DC,
在Rt△ABC中,AB=AC=1,
∴CB=![]() ,
,
∵BP=BP,AP=PD,
∴Rt△ABP≌Rt△DBP,
∴BD=AB=1,
∴CD=PD=AP=![]() 1,
1,
∴劣弧AD的长=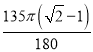 =
=![]() .
.
点睛: 本题考查了切线的判定、圆的作图以及弧长的计算,首先掌握切线的判定方法:①无交点,作垂线段,证半径;②有交点,作半径,证垂直;本题利用了第①种判定方法;并熟练掌握弧长计算公式:l=![]() (弧长为l,圆心角度数为n,圆的半径为R).
(弧长为l,圆心角度数为n,圆的半径为R).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在体育局的策划下,市体育馆将组织明星篮球赛,为此体育局推出两种购票方案(设购票张数为x,购票总价为y):
方案一:提供8000元赞助后,每张票的票价为50元;
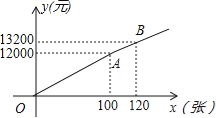
方案二:票价按图中的折线OAB所表示的函数关系确定.
(1)若购买120张票时,按方案一和方案二分别应付的购票款是多少?
(2)求方案二中y与x的函数关系式;
(3)至少买多少张票时选择方案一比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人去南方批发茶叶,在某地A批发市场以每包m元的价格进了40包茶叶,又到B批发市场时发现同样的茶叶比A批发市场要便宜,每包的价格仅为n元,因此他又在B批发市场进了60包同样的茶叶.如果他销售时以每包
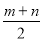 元的价格全部卖出这批茶叶,那么在不考虑其它因素的情况下他的这次买卖( )
元的价格全部卖出这批茶叶,那么在不考虑其它因素的情况下他的这次买卖( )A.一定盈利B.一定亏损
C.不盈不亏D.盈亏不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知单项式
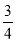 x3ya与单项式﹣5xby是同类项,c是多项式2mn﹣5m﹣n﹣3的次数.
x3ya与单项式﹣5xby是同类项,c是多项式2mn﹣5m﹣n﹣3的次数.(1)写出a,b,c的值;
(2)若关于x的二次三项式ax2+bx+c的值是3,求代数式2019﹣2x2﹣6x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个数轴上有A,B,C三点,它们所表示的数分别为2,﹣3,x.

(1)若点C是线段AB的中点,请直接写出x的值;
(2)若OC=OB﹣OA,求出x的值;
(3)若2AC+
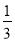 OB=7,求x的值.
OB=7,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)
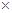 销售量】
销售量】(1)请根据他们的对话填写下表:
销售单价x(元/kg)
10
11
13
销售量y(kg)
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内,∠AOB=150°,∠COD=90°,OE平分∠BOD.
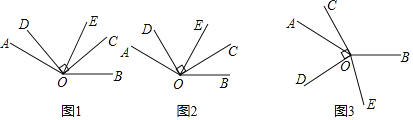
(1)当∠COD的位置如图1所示时,若∠COE=25°,则∠AOD= ;
(2)当∠COD的位置如图2所示时,若∠AOE=90°,则∠AOD= ;
(3)当∠COD的位置如图3所示时,若∠BOE=
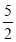 ∠AOC,求∠AOD的度数.
∠AOC,求∠AOD的度数.
相关试题

