【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图: 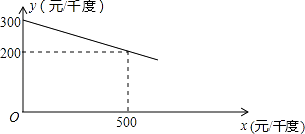
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=5m+600,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
参考答案:
【答案】
(1)解:设工厂每千度电产生利润y(元/千度)与电价x(元/千度)的函数解析式为:y=kx+b,
∵该函数图象过点(0,300),(500,200),
∴ ![]() ,
,
解得 ![]() .
.
所以y=﹣0.2x+300(x≥0),
当电价x=600元/千度时,该工厂消耗每千度电产生利润y=﹣0.2×600+300=180(元/千度)
(2)解:设工厂每天消耗电产生利润为w元,由题意得:
w=my=m(﹣0.2x+300)
=m[﹣0.2(5m+600)+300]
=﹣m2+180m
=﹣(m﹣90)2+8100,
在m≤90时,w随m的增大而最大,
由题意,m≤60,
∴当m=60时,w最大=﹣(60﹣90)2+8100=7200,
即当工厂每天消耗60千度电时,工厂每天消耗电产生利润为最大,最大利润为7200元
【解析】(1)设y=kx+b(k≠0),利用待定系数法求一次函数解析式解答即可;(2)根据利润=每天的用电量×每千度电产生利润y,然后整理得到W与m的关系式,再根据二次函数的最值问题解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
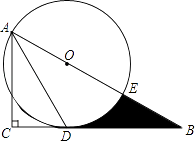
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π) -
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=﹣2x2的图象向上移动3个单位,所得到的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5x(2x2-3x+4);
(2)20172-2018×2016;
(3)
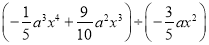 ;
; (4)(a+b)(a-b)+(a+b)2-2a2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2=0的解是( )
A.x=0B.无实数根C.1D.x1= x2=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;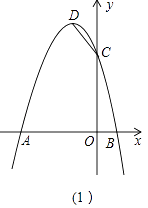
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.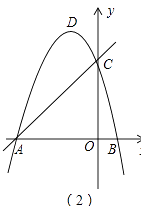
-
科目: 来源: 题型:
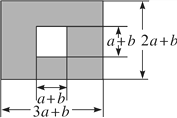
查看答案和解析>>【题目】如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地,中间将修建一座边长为(a+b)米的正方形雕像,规划部门计划将余下部分进行绿化.
(1)试用含a,b的式子表示绿化部分的面积(结果要化简);
(2)若a=3,b=2,请求出绿化部分的面积.
相关试题

