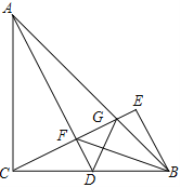
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD
求证:(1) △BEF为等腰直角三角形 ;(2) ∠ADC=∠BDG.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)连接DE,根据对称轴和线段垂直平分线的性质,求出CF=EF,CD=DE,推出CD=ED=BD,根据直角三角形的判定推出△BEF是直角三角形,求出∠AFC=∠BEC=∠ACD=90°,∠CAF=∠ECB,根据全等三角形的判定定理得出△ACF≌△CBE,根据全等三角形的性质得证;
(2)作∠ACB的平分线交AD于M,根据ASA推出△ACM≌△CBG得出∠ADC=∠M,CD=BM,根据SAS推出△DCM≌△DBG,求出∠M=∠BDG,即可得出答案.
试题解析:(1)连接DE,
∵点E、C关于AD对称,∴AD为CE的垂直平分线,
∴CD=DE,∵D为CB中点,∴CD=DE=DB,
∴∠DCE=∠CED,∠DEB=∠DBE,
∵∠DCE+∠CED+∠DEB+∠DBE=180°,
∴∠CEB=90°,
∵∠ECB+∠ACF=90°,∠CAF+∠ACF=90°,
∴∠ECB=∠CAF,
在△ACF和△CBE中,
∵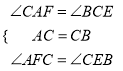
∴△ACF≌△CBE(AAS),
∴CF=BE,右∵CF=EF,∴EF=EB,
∴△EFB为等腰直角三角形.
(2)作∠ACB的平分线交AD于M,
在△ACM和△CBG中,
∵
∴△ACM≌△CBG(ASA),
∴CM=BG,
在△DCM和△DBG中,
∵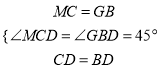
∴△DCM≌△DBG(SAS),
∴∠ADC=∠GDB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a﹣1|=9,|b+2|=6,且a+b<0,求a﹣b的值_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年一班的20名男生在进行体育加试测试中,所做人体向上的个数如下表:
个数
15
14
13
12
11
人数
4
7
4
3
2
则该校九年一班男生做人体向上的中位数是个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在体育课的跳远比赛中,以4.00米为标准,若小东跳出了4.22米,可记做+0.22,那么小东跳出了3.85米,记作 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,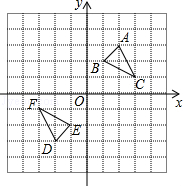
解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程(a﹣5)x2﹣4x﹣1=0有实数根,则实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
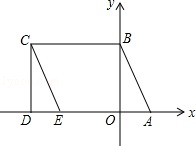
(1)直接写出点E的坐标;
(2)在四边形ABCD中,点P从点B出发,沿BC→CD移动.若点P的速度为每秒1个单位长度,运动时间为t秒,请解决以下问题,并说明你的理由:
①当t为多少秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标(用含t的式子表示)
相关试题

