搜索
【题目】小王沿街匀速行走，发现每隔6分钟从背后驶过一辆18路公交车，每隔3分钟从迎面驶来一辆18路公交车．假设每辆18路公交车行驶速度相同，而且18路公交车总站每隔固定时间发一辆车，那么发车间隔的时间是（ ）
A. 3分钟 B. 4分钟 C. 5分钟 D. 6分钟
参考答案：
【答案】B
【解析】
设同向行驶的相邻两车的距离及车、小王的速度为未知数，等量关系为：6×车速﹣6×小王的速度=同向行驶的相邻两车的距离；3×车速+3×小王的速度=同向行驶的相邻两车的距离；把相关数值代入可得同向行驶的相邻两车的距离及车的速度关系式，相除可得所求时间．
设18路公交车的速度是x米/分，小王行走的速度是y米/分，同向行驶的相邻两车的间距为s米．
每隔6分钟从背后开过一辆18路公交车，则6x﹣6y=s．①
每隔3分钟从迎面驶来一辆18路公交车，则3x+3y=s．②
由①，②可得s=4x，所以
．
即18路公交车总站发车间隔的时间是4分钟．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD和正方形AEFG有一个公共点A，点G、E分别在线段AD、AB上．
（1）连接DF、BF，若将正方形AEFG绕点A按顺时针方向旋转，判断命题“在旋转的过程中，线段DF与BF的长始终相等”是否正确？答： ．
（2）若将正方形AEFG绕点A按顺时针方向旋转，连接DG，在旋转过程中，你能否找到一条线段的长与线段DG的长始终相等？并以图为例说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+m．
（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；
（2）如图，二次函数的图象过点A（3，0），与y轴交于点B，直线AB与这个二次函数图象的对称轴交于点P，求点P的坐标．
（3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”.如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N.试解答下列问题：
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系： ；
（2）图2中，当∠D=50度，∠B=40度时，求∠P的度数.
（3）图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完．这两种节能灯的进价、售价如下表：
进价（元/只）
售价（元/只）
甲种节能灯
30
40
甲种节能灯
35
50
（1）求幸福商场甲、乙两种节能灯各购进了多少只？
（2）全部售完100只节能灯后，商场共计获利多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一个三位数，其个位数加上十位数等于百位数，可表示为t=100（x+y）+10y+x，则称实数t为“加成数”，将t的百位作为个位，个位作为十位，十位作为百位，组成一个新的三位数h．规定q=t﹣h，f（m）=
，例如：321是一个“加成数”，将其百位作为个位，个位作为十位，十位作为百位，得到的数h=213，∴q=321﹣213=108，f（m）=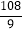
=12．（1）当f（m）最小时，求此时对应的“加成数”的值；
（2）若f（m）是24的倍数，则称f（m）是“节气数”，猜想这样的“节气数”有多少个，并求出所有的“节气数”．
-
科目： 来源： 题型：
查看答案和解析>>【题目】现有一组有规律排列的数：1、﹣1、
、﹣、
、﹣、1、﹣1、、﹣、、﹣…其中，1、﹣1、、﹣、、﹣这六个数按此规律重复出现，问：（1）第50个数是什么数？
（2）把从第1个数开始的前2017个数相加，结果是多少？
（3）从第1个数起，把连续若干个数的平方加起来，如果和为520，则共有多少个数的平方相加？
相关试题
