【题目】已知直线l1∥l2 , 且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点如图1) 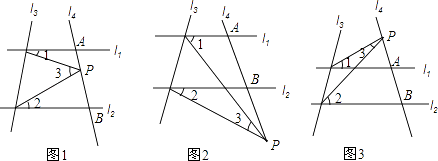
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
参考答案:
【答案】
(1)解:延长DP交直线l2于E,如图1,
∵直线 l1∥l2,
∴∠DEC=∠1,
∵∠3=∠DEC+∠2,
∴∠3=∠2+∠1;
(2)解:不变化,∠3=∠1+∠2,
理由是:∵直线 l1∥l2,
∴∠DEC=∠1,
∴∠3=∠2+∠DEC=∠1+∠2,
(3)解:①当点P在射线AB上运动时,如图2,
∵直线 l1∥l2,
∴∠PFB=∠1,
∴∠PFB=∠2+∠3,
∴∠1=∠2+∠3,
②如图3,当点P在射线BA上运动时,
∵直线 l1∥l2,
∴∠PGA=∠2,
∴∠PGA=∠1+∠3,
∴∠2=∠1+∠3.
【解析】(1)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;(2)延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;(3)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可;(4)画出图形,延长DP交直线l2于E,根据平行线得出∠1=∠DEC,根据三角形外角性质求出即可.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
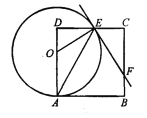
查看答案和解析>>【题目】如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于 点F,且∠CEF=2∠DAE.
(1)求证:直线EF为⊙O的切线;
(2)在点O的运动过程中,设DE=x,解决下列问题:
①求OD·CF的最大值,并求此时半径的长;
②试猜想并证明△CEF的周长为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x-2=2-x的解是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿,把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC,BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin530≈0.8,cos530≈0.6,tan530≈1.3)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一商店把某种品牌的裤子按标价的八折出售,仍可获利20%,若该品牌的裤子每条的进价是180元,则标价是每件______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件上衣,每件原价500元,第一次降价后,销售甚慢,于是再次进行大幅降价,第二次降价的百分率是第一次降价的百分率的2倍,结果这批上衣以每件240元的价格迅速售出,求两次降价的百分率各是多少.
相关试题

