【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】
利用平行四边形的性质以及全等三角形的判定分别分得出即可.
A、当BE=FD,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,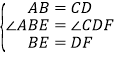 ,
,
∴△ABE≌△CDF(SAS);故该选项不符合题意,
B、当AE=CF无法得出△ABE≌△CDF,故此选项符合题意
C、当BF=ED,
∴BE=DF,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
∵BF=ED,
∴BF-EF=ED-EF,即BE=DF,
在△ABE和△CDF中,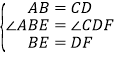 ,
,
∴△ABE≌△CDF(SAS);故该选项不符合题意,
D、当∠1=∠2,
∵平行四边形ABCD中,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,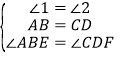 ,
,
∴△ABE≌△CDF(ASA),故该选项不符合题意,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.

(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】模型建立:
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.

求证:△BEC≌△CDA.
模型应用:
(2)已知直线l1:y=
 x+4与y轴交与A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.
x+4与y轴交与A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式.(3)如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x-6上的一点,若△APD是不以A为直角顶点的等腰Rt△,请直接写出点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司销售一种进价为
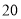 元/个的计算器,其销售量
元/个的计算器,其销售量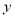 (万个)与销售价格
(万个)与销售价格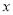 (元/个)的变化如下表:
(元/个)的变化如下表:价格
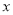 (元/个)
(元/个)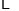
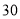
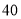
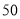
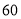
销售量
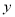 (万个)
(万个)
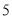
同时,销售过程中的其他开支(不含造价)总计
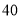 万元.
万元.(
 )观察并分析表中的
)观察并分析表中的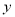 与
与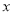 之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出
之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出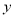 (万个)与
(万个)与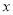 (元/个)的函数解析式.
(元/个)的函数解析式.(
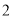 )求出该公司销售这种计算器的净得利润
)求出该公司销售这种计算器的净得利润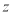 (万个)与销售价格
(万个)与销售价格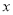 (元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?(
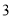 )该公司要求净得利润不能低于
)该公司要求净得利润不能低于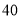 万元,请写出销售价格
万元,请写出销售价格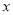 (元/个)的取值范围.
(元/个)的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
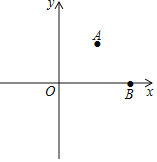
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P.则下列结论:(1)AD+BE=AC;(2)AD2+BE2=DE2;(3)△ABC的面积等于四边形CDOE面积的2倍;(4)OD=OE.其中正确的结论有( )
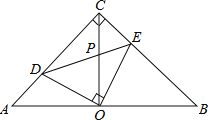
A.
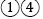 B.
B. 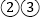 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,点A(-3,0),点B(3,0),点D是y轴上的一个动点,连接BD,将线段BD绕点B逆时针旋转60°,得到线段BE,连接DE,得到△BDE,则OE的最小值为______.
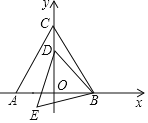
相关试题

