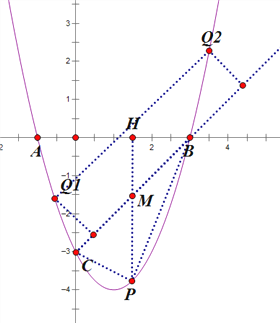
【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当△BCP的面积最大时,求点P的坐标和△BCP的最大面积.
(3)当△BCP的面积最大时,在抛物线上是否点Q(异于点P),使△BCQ的面积等于△BCP,若存在,求出点Q的坐标,若不存在,请说明理由.

参考答案:
【答案】(1)y=x2﹣2x﹣3;(2)P点坐标为(![]() ,﹣
,﹣![]() )时,△BCP的面积最大,最大面积为
)时,△BCP的面积最大,最大面积为![]() ;(3)存在,Q点坐标为
;(3)存在,Q点坐标为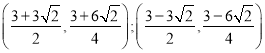
【解析】试题分析:(1)直接用代入法求函数的解析式;(2)连接BC,过点P作y轴的平行线,交BC于点M,交x轴于点H,求直线BC的函数解析式,设P点坐标为(x,x2﹣2x﹣3),则M点坐标为(x,x﹣3),则PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,由S△PBC=![]() PM
PM![]() OH+
OH+![]() PM
PM![]() HB=
HB=![]() PM(OH+HB)=
PM(OH+HB)=![]() PM
PM![]() OB=
OB=![]() PM,当PM有最大值时,△PBC的面积最大,由PM=﹣x2+3x=-(x﹣
PM,当PM有最大值时,△PBC的面积最大,由PM=﹣x2+3x=-(x﹣![]() )2+
)2+![]() 可得,当x=
可得,当x=![]() 时,有最大值PM=
时,有最大值PM=![]() ,则S△PBC=
,则S△PBC=![]() ×
×![]() =
=![]() ,把x=
,把x=![]() 代入 x2﹣2x﹣3=﹣
代入 x2﹣2x﹣3=﹣![]() ,则点P的坐标为(
,则点P的坐标为(![]() ,﹣
,﹣![]() );(3)求出直线Q1Q2的解析式,再求它与二次函数交点坐标即为所求;
);(3)求出直线Q1Q2的解析式,再求它与二次函数交点坐标即为所求;
试题解析:
(1)把B、C两点坐标代入抛物线解析式可得![]() ,解得
,解得![]()
![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3;
(2) 连接BC,过点P作y轴的平行线,交BC于点M,交x轴于点H,如图所示:
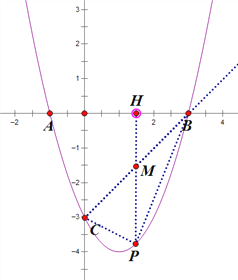
在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=﹣1或x=3,则点B的坐标为(3,0),令x=0,y=-3,则点C的坐标为(0,-3),
∵B(3,0),C(0,﹣3),
∴直线BC解析式为y=x﹣3,
设P点坐标为(x,x2﹣2x﹣3),则M点坐标为(x,x﹣3),
∵P点在第四限,
∴PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,
∴S△PBC=![]() PM
PM![]() OH+
OH+![]() PM
PM![]() HB=
HB=![]() PM(OH+HB)=
PM(OH+HB)=![]() PM
PM![]() OB=
OB=![]() PM,
PM,
∴当PM有最大值时,△PBC的面积最大,
∵PM=﹣x2+3x=﹣(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,有最大值PM=
时,有最大值PM=![]() ,则S△PBC=
,则S△PBC=![]() ×
×![]() =
=![]() ,
,
此时P点坐标为(![]() ,﹣
,﹣![]() ), S△PBC=
), S△PBC=![]() ,
,
即当P点坐标为(![]() ,﹣
,﹣![]() )时,△BCP的面积最大,最大面积为
)时,△BCP的面积最大,最大面积为![]() ;
;
(3)∵△BCP的面积面积为![]()
∴△BCP的高是![]() ,
,
作直线BC的平行的直线Q1Q2,且距离直线BC为![]() ,
,
∵直线BC的函数为y=x-3,
∴直线Q1Q2的解析式为y=x-![]() ,
,
又∵二次函数的解析线为y=x2﹣2x﹣3,
∴两条直线交点Q2坐标为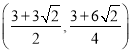 ,Q1的坐标为
,Q1的坐标为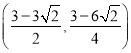 。
。
∴存在,Q点坐标为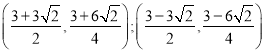 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为“方便交通,绿色出行”,人们常选择以共享单车作为代步工具、图(1)所示的是一辆自行车的实物图.图(2)是这辆自行车的部分几何示意图,其中车架档AC与CD的长分别为45cm和60cm,且它们互相垂直,座杆CE的长为20cm.点A、C、E在同一条直线上,且∠CAB=75°.
(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732)
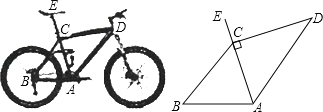
图(1) 图(2)
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+mx+n=0的两个实数根分别为x1=﹣2,x2=4,则m+n的值是( )
A.﹣10
B.10
C.﹣6
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果用+3米表示高出警戒水位3米,那么低于警戒水位5米记作( )
A.+5米
B.﹣5米
C.0米
D.﹣10米 -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程为ax2+bx+6=0(a≠0)的解是x=1,则2016﹣a﹣b的值是( )
A.2020
B.2008
C.2014
D.2022 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于x的方程中,一定是一元二次方程的为( )
A. ax2+bx+c=0B. x2 -2=(x+3)2C. x2 +3y 5=0D. x2-1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )
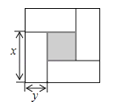
A.x+y=7
B.x﹣y=2
C.x2﹣y2=4
D.4xy+4=49
相关试题

