【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
(1)填空:A,B两地相距千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?相遇处离C站的路程是多少千米?
参考答案:
【答案】
(1)420
(2)解:由图可知货车的速度为60÷2=30千米/小时,
货车到达A地一共需要2+360÷30=14小时,
设y2=kx+b,代入点(2,0)、(14,360)得
![]() ,
,
解得k=30,b=-60 ∴y2=30x-60,(x≥2)
(3)解:设客车离C站的路程y1与行驶时间x之间的函数表达式为y1=k1x+b1,根据题意得
![]()
解得k1=-60,b1=360 y1=-60x+360 由y1=y2得 30x-60=-60x+360 解得x= ![]()
![]() (千米)
(千米)
答:客、货两车在出发后 ![]() 小时相遇.相遇处离C站的路程是80千米.
小时相遇.相遇处离C站的路程是80千米.
【解析】解:(1)由题意可知:B、C之间的距离为60千米,A、C之间的距离为360千米,所以A,B两地相距360+60=420千米;
(1)由y轴上的初始值,可知二车距C站的距离,两数相加,即是A、B两地的距离;(2)DP段的一次函数图像,可用待定系数法求出;(3)相遇处时间就是DP 段与客车图象的交点横坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2(x-2)-3(x+1)=-3
-
科目: 来源: 题型:
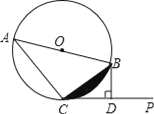
查看答案和解析>>【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
(1)求证:CB2=ABDB;
(2)若⊙O的半径为2,∠BCP=30°,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列现象是数学中的平移的是( )
A. 小朋友荡秋千
B. 碟片在光驱中运行
C. “神舟”十号宇宙飞船绕地球运动
D. 瓶装饮料在传送带上移动
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点(﹣1,5)关于x轴的对称点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】某种药原来每瓶售价为40元,经过两次降价,现在每瓶售价为25.6元,则平均每次降价的百分率是_____________.
-
科目: 来源: 题型:
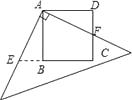
查看答案和解析>>【题目】有一块边长为4的正方形ABCD,将一块足够大的直角三角板如图放置, CB延长线与直角边交于点E.则四边形AECF的面积是 .
相关试题

