【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .
.
例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=![]() .
.
⑴如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
⑵如果一个两位正整数t,t =10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为54,那么我们称这个数t为“吉祥数”,求所有的“吉祥数”;
⑶在⑵所得“吉祥数”中,求 F(t)的最大值.
参考答案:
【答案】(1)见解析;(2)17,28,39;(3)![]()
【解析】(1)对任意一个完全平方数m,设![]() (
(![]() 为正整数),找出m的最佳分解,确定出
为正整数),找出m的最佳分解,确定出![]() 的值即可;
的值即可;
(2)设交换t的个位上数与十位上的数得到的新数为t′,则![]() ,根据“吉祥数”的定义确定出x与y的关系式,进而求出所求即可;
,根据“吉祥数”的定义确定出x与y的关系式,进而求出所求即可;
(3)利用“吉祥数”的定义分别求出各自的值,进而确定出![]() 的最大值即可.
的最大值即可.
(1)对任意一个完全平方数m,设m=n2(n为正整数),
∵|n-n|=0,
∴n×n是m的最佳分解,
∴对任意一个完全平方数m,总有F(m)=![]() =1;
=1;
(2)设交换t的个位上的数与十位上的数得到的新数为t′,则![]()
∵t为“吉祥数”,
∴![]()
∴![]()
∵![]() x,y为自然数,
x,y为自然数,
∴“吉祥数”有:17,28,39,
(3)F(17)=![]() ,F(28)=
,F(28)=![]() ,F(39)=
,F(39)=![]() ,
,
∵![]() >
>![]() >
>![]() ,
,
∴所有“吉祥数”中,F(t)的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在函数y=
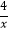 (x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=
(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y= 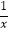 图象于点B,C,直线BC与坐标轴的交点为D,E.
图象于点B,C,直线BC与坐标轴的交点为D,E.
(1)当点C的横坐标为1时,求点B的坐标;
(2)试问:当点A在函数y=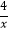 (x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(3)试说明:当点A在函数y=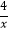 (x>0)图象上运动时,线段BD与CE的长始终相等.
(x>0)图象上运动时,线段BD与CE的长始终相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(a+1)(a﹣1)=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按程序x平方+x÷x﹣3x进行运算后,结果用x的代数式表示是_____.(填入运算结果的最简形式)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某工厂计划用库存的302m3木料为某学校生产500套桌椅,供该校1250名学生使用,该厂生产的桌椅分为A,B两种型号,有关数据如下:
桌椅型号
一套桌椅所坐学生人数(单位:人)
生产一套桌椅所需木材(单位:m3)
一套桌椅的生产成本(单位:元)
一套桌椅的运费(单位:元)
A
2
0.5
100
2
B
3
0.7
120
4
设生产A型桌椅x(套),生产全部桌椅并运往该校的总费用(总费用=生产成本+运费)为y元.
(1)求y与x之间的关系式,并指出x的取值范围;
(2)当总费用y最小时,求相应的x值及此时y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)2018×2020﹣20192;(2)3x5x2﹣5(x3)3÷x2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料,回答问题:已知(x-2)(6+2x)>0,求x的取值范围.
解:根据题意,得
 或
或
分别解这两个不等式组,得x>2或x<-3.
故当x>2或x<-3时,(x-2)(6+2x)>0.
(1)由(x-2)(6+2x)>0,得出不等式组
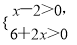 或
或 体现了____思想.
体现了____思想.(2)试利用上述方法,求不等式(x-3)(1-x)<0的解集.
附加题(15分,不计入总分)
相关试题

