【题目】平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动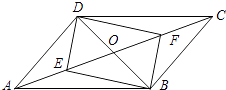
(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=18cm,当运动时间t为多少时,以D、E、B、F为顶点的四边形为矩形.
参考答案:
【答案】
(1)
解:四边形DEBF是平行四边形.
理由:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,
∴AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形
(2)
解:根据题意得:AE=CF=2tcm或18﹣2tcm,
∵四边形DEBF是平行四边形,
∴当EF=BD时,四边形DEBF为矩形.
即AC﹣AE﹣CF=BD或AE+CF﹣AC=EF,
∴18﹣2t﹣2t=10或2t+2t﹣18=10,
解得:t=2或t=7
∴当运动时间t为2s或7s时,四边形DEBF为矩形
【解析】(1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:18﹣2t﹣2t=10,继而求得答案.
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质和矩形的判定方法的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产某种商品每件成本为20元,这种商品在未来40天内的日销售量y(件)与时间x(天)的关系如下表:
时间x(天)
1
3
6
10
...
日销售量y(件)
94
90
84
76
...
未来40天内,前20天每天的价格m(元/件)与时间x(天)的函数关系式为
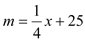 (1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).
(1≤x≤20),后20天每天的价格为30元/件(21≤x≤40).(1)分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的y(件)与x(天)之间的函数关系式.
(2)当1≤x≤20时,设日销售利润为W元,求出W与x的函数关系式.
(3)在未来40天中,哪一天的日销售利润最大,最大日销售利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.平行四边形B.矩形C.正三角形D.正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年我国大学生毕业人数将达到7 490 000人,这个数据用科学记数法表示为( )
A.7.49×107
B.7.49×106
C.74.9×105
D.0.749×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点A、B分别在函数y1=
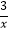 (x>0)与y2=﹣
(x>0)与y2=﹣ 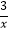 (x<0)的图象上,A、B的横坐标分别为a、b.
(x<0)的图象上,A、B的横坐标分别为a、b.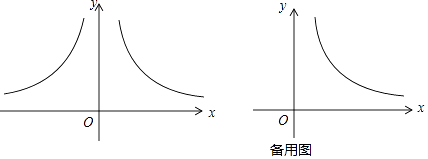
(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;
(3)作边长为2的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于3的任意实数a,CD边与函数y1=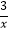 (x>0)的图象都有交点,请说明理由.
(x>0)的图象都有交点,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解结果正确的是( )
A.a2﹣9=(a+3)(a﹣3)B.x2﹣x=x(x2﹣1)
C.x2+2x+4=(x+2)2D.﹣4m3+12m2=﹣m2(4m﹣12)
-
科目: 来源: 题型:
查看答案和解析>>【题目】用2,3,4,5这四个数字,使计算的结果为24,请列出1个符合要求的算式____________(可运用加、减、乘、除、乘方)
相关试题

