【题目】如图，中，，，将绕点逆时针旋转()得，若交于点，当__________时，为等腰三角形．

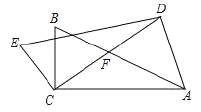
【答案】或

【解析】

根据旋转的性质可得：DC＝AC，根据等边对等角可知：∠CDA＝∠CAD，再表示出∠DAF，根据三角形外角的性质可表示出∠DFA，然后分①∠ADF＝∠DAF，②∠ADF＝∠DFA，③∠DAF＝∠DFA三种情况讨论求解．

∵△ABC绕点C按逆时针方向旋转()得△DEC，

∴∠DCA＝，DC＝AC，

∴∠CDA＝∠CAD＝,

∵∠BAC＝24°，

∴∠DAF＝∠CAD－∠BAC＝

根据三角形的外角性质可得：∠DFA＝∠BAC＋∠DCA＝，

△ADF是等腰三角形，分三种情况讨论：

①当∠ADF＝∠DAF时， ，此时无解；

②当∠ADF＝∠DFA时，，解得：；

③当∠DAF＝∠DFA时，，解得：；

综上所述，旋转角度数为或

故答案为：或

关闭