【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.

(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
参考答案:
【答案】详见解析.
【解析】试题分析:(1)、根据旋转图形的性质可得:CD=CE,∠DCE=90°,根据∠ACB=90°得出∠BCD=90°-∠ACD=∠FCE,结合已知条件得出三角形全等;(2)、根据全等得出∠BDC=∠E,∠BCD=∠FCE,从而得出∠DCE=90°,然后根据EF∥CD得出∠BDC=90°.
试题解析:(1)、∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=90°-∠ACD=∠FCE,
在△BCD和△FCE中, CB=CF
∵BCD=∠FCE,CD=CE,CB=CF,∠BCD=∠FCE
∴△BCD≌△FCE(SAS).
(2)、由(1)可知△BCD≌△FCE,
∴∠BDC=∠E,∠BCD=∠FCE,
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,
∵EF∥CD,
∴∠E=180°-∠DCE=90°,
∴∠BDC=90°.
-
科目: 来源: 题型:
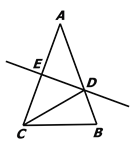
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程3xn﹣1+(m﹣2)x2﹣5=0是一元一次方程,则m、n的值分别为( )
A. m=1,n=2 B. m=2,n=2 C. m=2,n=1 D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
-
科目: 来源: 题型:
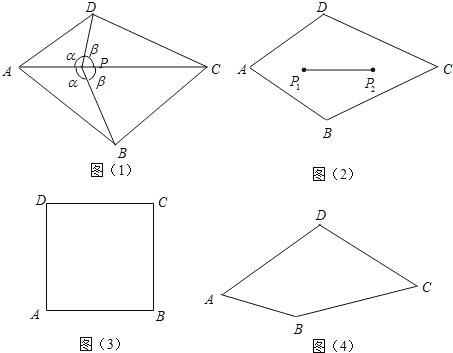
查看答案和解析>>【题目】如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.
【1】在图(3)正方形ABCD内画一个半等角点P,且满足α≠β;
【2】在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法);
【3】若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是方程8﹣2x=ax的解,则a=
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元一次方程2x+a﹣4=0的解是x=﹣2,则a的值是( )
A. ﹣8 B. 8 C. 2 D. 0
相关试题

