【题目】如图所示,电工李师傅借助梯子安装天花板上距地面2 .90m的顶灯.已知梯子由两个相同的矩形面组成,每个矩形面的长都被六条踏板七等分,使用时梯脚的固定跨度为1m.矩形面与地面所成的角α为78°.李师傅的身高为l.78m,当他攀升到头顶距天花板0.05~0.20m时,安装起来比较方便.请问他站立在梯子的第几级踏板上安装比较方便?,请你通过计算判断说明.
(参考数据:sin78°≈0.98,cos78°≈0.21,tan78°≈4.70)

参考答案:
【答案】第三级踏板,理由见解析.
【解析】
试题分析:本题中问题的解决要弄清楚电工李师傅所站的地方离地面的高度,通过解直角三角形来解决.
首先可求得点A离地面的距离,再用相似三角形对应边成比例,或者同角三角函数的比例,求得第三级离地面的高度,即可求得他头顶离房顶的距离.
试题解析:过点A作AE⊥BC于点E,过点D作DF⊥BC于点F.

∵AB=AC,∴CE=![]() BC=0.5.
BC=0.5.
在Rt△AEC和Rt△DFC中,
∵tan78°=![]() ,
,
∴AE=EC×tan78°≈0.5×4.70=2.35.
又∵sinα=![]() ,DF=
,DF=![]() ×AE=
×AE=![]() ×AE≈1.007.
×AE≈1.007.
∴李师傅站在第三级踏板上时,头顶距地面高度约为:1.007+1.78=2.787.
头顶与天花板的距离约为:2.90-2.787≈0.11.
∵0.05<0.11<0.20,
∴他安装比较方便.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(﹣3)﹣(﹣9)的结果等于( )
A. 12 B. ﹣12 C. 6 D. ﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个以3和-4为根的一元二次方程:_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店经销一种品牌服装,平均每天可销售20件,每件赢利44元,经市场预测发现:在每件降价不超过10元的情况下,若每件降价1元,则每天可多销售5件,若该专卖店要使该品牌服装每天的赢利为1600元,则每件应降价_________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.某中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:
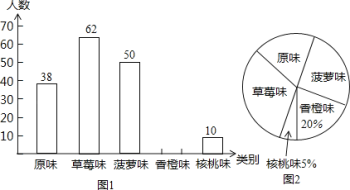
(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“草莓味”牛奶的学生人数在扇形统计图2中所占圆心角的度数;
(3)该校共有2400名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.

相关试题

