【题目】已知一次函数y=﹣2x﹣4
(1)根据关系式画出函数的图象.
(2)求出图象与x轴、y轴的交点A、B的坐标.
(3)求A、B两点间的距离.
(4)求出△AOB的面积.
(5)y的值随x值的增大怎样变化?
参考答案:
【答案】
(1)解:函数图象如下:
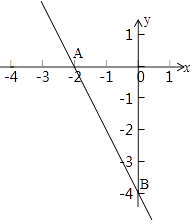
(2)解:令y=0得,﹣2x﹣4=0,
解得:x=﹣2,
∴点A(﹣2,0),
令x=0得y=﹣4,
∴点B(0,﹣4)
(3)解:∵OA=2,OB=4,
∴AB= ![]() =
= ![]() =2
=2 ![]()
(4)解:S△AOB= ![]() OAOB=
OAOB= ![]() ×2×4=4
×2×4=4
(5)解:∵k=﹣2<0,
∴y随x的增大而减小
【解析】(1)根据解析式画出图象即可;(2)分别令y=0和x=0求出另一变量的值即可得;(3)根据勾股定理可得;(4)根据三角形的面积公式可得;(5)根据一次函数的图象或性质可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=5x+b2-9的图象经过原点,则b=____.
-
科目: 来源: 题型:
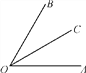
查看答案和解析>>【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB=60°时,求∠AOC的度数;
(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;
(3)当∠AOB=α时,∠EOC=90°,直接写出∠AOE的度数.(用含α的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图1.
①若∠AOC=60°,求∠DOE的度数;
②若∠AOC=α,直接写出∠DOE的度数(用含α的式子表示);
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置,试探究∠DOE和∠AOC的度数之间的关系,写出你的结论,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用一副三角尺,不能画出的角是( )
A. 15° 角 B. 75° 角 C. 100° 角 D. 135° 角
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2×(﹣3)+(﹣40)÷8+32 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法写出数0.05129(精确到百分位)的近似数是 .
相关试题

