【题目】如图,四边形ABCD中,AD∥BC,∠ADC=α,P为直线CD上一动点,点M在线段BC上,连MP,∠MPD=β 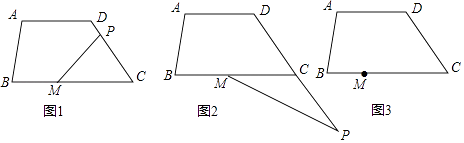
(1)如图,若MP⊥CD,α=120°,则∠BMP=;
(2)如图,当P点在DC延长线上时,∠BMP=;
(3)如图,当P点在CD延长线上时,请画出图形,写出∠BMP、β、α之间的数量关系,并证明你的结论.
参考答案:
【答案】
(1)150°
(2)60°+β
(3)解:∵AD∥BC,
∴∠BCP=∠ADC=α,
在△CMP中,∠CMP=180°﹣∠BCP﹣∠MPD=180°﹣α﹣β,
∴∠BMP=180°﹣∠CMP=180°﹣(60°﹣α)=α+β.
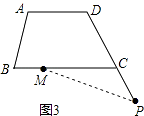
【解析】解:(1)∵AD∥BC, ∴∠C=180°﹣∠ADC=180°﹣120°=60°,
∵MP⊥CD,
∴∠CMP=90°﹣∠C=90°﹣60°=30°,
∴∠BMP=180°﹣∠CMP=180°﹣30°=150°;(2)∵AD∥BC,
∴∠C=180°﹣∠ADC=180°﹣120°=60°,
在△CMP中,∠CMP=180°﹣∠C﹣∠MPD=180°﹣60°﹣β=120°﹣β,
∴∠BMP=180°﹣∠CMP=180°﹣(120°﹣β)=60°+β;
所以答案是:(1)150°;(2)60°+β;
【考点精析】根据题目的已知条件,利用平行线的性质的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,三个顶点A、B、C的坐标分别是(﹣1,4)、(﹣4,﹣1)、(1,1).将△ABC向右平移5个单位长度,再向上平移1个单位长度,得到△A′BC

(1)请画出平移后的,并写出的坐标
(2)若在第四象限内有一点M(4,m),是否存在点M,使得四边形A′OMB′的面积等于△ABC的面积的一半?若存在,请求出点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,D为AB上一点,E为AC上一点,添加一个条件(只能填一个)可以使得△ABC与△ADE相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(4,﹣3),则点P到y轴的距离为
-
科目: 来源: 题型:
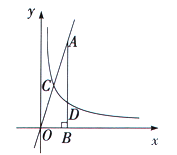
查看答案和解析>>【题目】如图,反比例函数
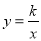 (
(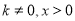 ,)的图象与直线
,)的图象与直线 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算-3(x-2y)+4(x-2y)的结果是( )
A. -x-2y B. x+2y C. x-2y D. -x+2y
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、B、C、E、P均在坐标轴上,A(0,3)、B(﹣4,0)、P(0,﹣3),点C是线段OP(不包含O、P)上一动点,AB∥CE,延长CE到D,使CD=BA
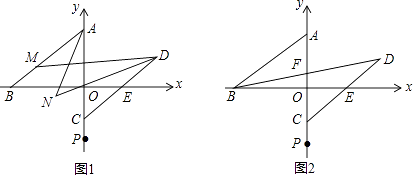
(1)如图,点M在线段AB上,连MD,∠MAO与∠MDC的平分线交于N.若∠BAO=α,∠BMD=130°,则∠AND的度数为
(2)如图,连BD交y轴于F.若OC=2OF,求点C的坐标
(3)如图,连BD交y轴于F,在点C运动的过程中,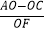 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.
相关试题

