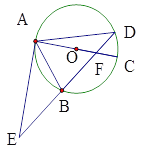
【题目】如图,已知⊙O的直径AC与弦BD相交于点F,点E是DB延长线上的一点,∠EAB=∠ADB;
(1)求证:AE是⊙O的切线;
(2)已知点B是EF的中点,求证:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)、连接CD,根据直径所对的圆周角为直角得出∠ADB+∠EDC=90°,根据同弧所对的圆周角相等得出∠BAC=∠EDC,然后结合已知条件得出∠EAB+∠BAC=90°,从而说明切线;(2)、连接BC,根据直径的性质得出∠ABC=90°,根据B是EF的中点得出AB=EF,即∠BAC=∠AFE,则得出三角形相似;(3)、根据三角形相似得出![]() ,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入
,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入![]() 求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
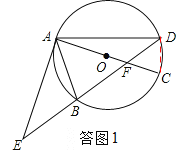
试题解析:(1)、如答图1,连接CD, ∵AC是⊙O的直径,∴∠ADC=90°. ∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB, ∴∠BAC=∠EAB+∠BAC=90°. ∴EA是⊙O的切线.
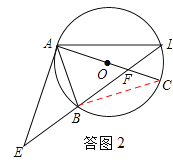
(2)、如答图2,连接BC, ∵AC是⊙O的直径,∴∠ABC=90°. ∴∠CBA=∠ABC=90°.
∵B是EF的中点,∴在Rt△EAF中,AB=BF. ∴∠BAC=∠AFE. ∴△EAF∽△CBA.
(3)、∵△EAF∽△CBA,∴![]() . ∵AF=4,CF=2, ∴AC=6,EF=2AB.
. ∵AF=4,CF=2, ∴AC=6,EF=2AB.
∴![]() ,解得AB=2
,解得AB=2![]() .∴EF=4
.∴EF=4![]() .
.
∴AE=![]() .
.
-
科目: 来源: 题型:
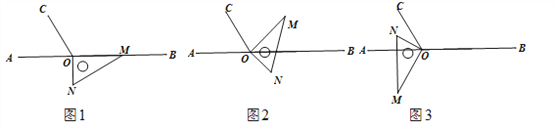
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM=_______度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.探究∠AOM与∠NOC之间数量关系,并说明你的理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是多少秒?(直接写出答案即可,不必说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
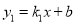 与反比例函数
与反比例函数 的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.
的图象相交于A,B两点,且与坐标轴的交点为(﹣6,0),(0,6),点B的横坐标为﹣4.(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式
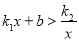 的解.
的解.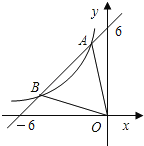
-
科目: 来源: 题型:
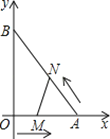
查看答案和解析>>【题目】如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒
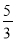 个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).
个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).(1)当t=3秒时,直接写出点N的坐标;
(2)在此运动的过程中,△MNA的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由;
(3)当t为何值时,△MNA是一个等腰三角形?
-
科目: 来源: 题型:
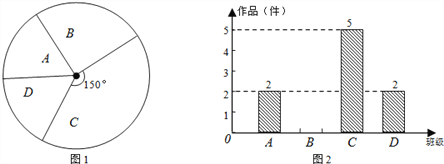
查看答案和解析>>【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)李老师采取的调查方式是 (填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共 件,其中B班征集到作品为 件,请把图2补充完整.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要在抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在频率分布直方图中,以下说法错误的是( )
A.每个小长方形的面积等于频数
B.每个小长方形的面积等于频率
C.频率=频数÷数据总数
D.各个小长方形面积和等于1 -
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据﹣1、2、3、4的极差是( )
A.5
B.4
C.3
D.2
相关试题

