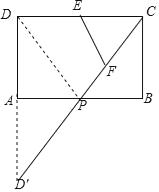
【题目】如图,矩形△ABCD中,AB=2,AD=1,E为CD中点,P为AB边上一动点(含端点),F为CP中点,则△CEF的周长最小值为_____.

参考答案:
【答案】![]() +1.
+1.
【解析】
根据三角形的中位线的性质得到EF=![]() PD,得到C△CEF=CE+CF+EF=CE+
PD,得到C△CEF=CE+CF+EF=CE+![]() (CP+PD)=
(CP+PD)=![]() (CD+PC+PD)=
(CD+PC+PD)=![]() C△CDP,当△CDP的周长最小时,△CEF的周长最小;即PC+PD的值最小时,△CEF的周长最小;如图,作D关于AB的对称点D′,连接CD′交AB于P,于是得到结论.
C△CDP,当△CDP的周长最小时,△CEF的周长最小;即PC+PD的值最小时,△CEF的周长最小;如图,作D关于AB的对称点D′,连接CD′交AB于P,于是得到结论.
解:∵E为CD中点,F为CP中点,
∴EF=![]() PD,
PD,
∴C△CEF=CE+CF+EF=CE+![]() (CP+PD)=
(CP+PD)=![]() (CD+PC+PD)=
(CD+PC+PD)=![]() C△CDP,
C△CDP,
∴当△CDP的周长最小时,△CEF的周长最小;
即PC+PD的值最小时,△CEF的周长最小;
如图,作D关于AB的对称点D′,连接CD′交AB于P,
∵AD=AD′=BC,AD′∥BC,
∴四边形AD′BC是平行四边形,
∴AP=PB=1,PD′=PC,
∴CP=PD=![]() ,
,
∴C△CEF=![]() C△CDP=
C△CDP=![]() +1,
+1,
故答案为:![]() +1.
+1.
-
科目: 来源: 题型:
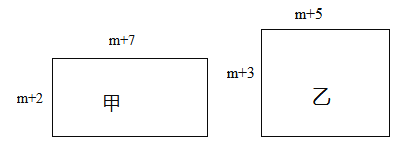
查看答案和解析>>【题目】已知有甲、乙两个长方形,它们的边长如图所示(m为正整数),面积分别为S1、S2.
(1)请比较S1与S2的大小: S1 S2;
(2)若一个正方形与甲的周长相等.
①求该正方形的边长(用含m的代数式表示);
②若该正方形的面积为S3,试探究:S3与S1的差(即S3﹣S1)是否为常数?若为常数,求出这个常数;如果不是,请说明理由;
(3)若满足条件0<n<|S1﹣S2|的整数n有且只有8个,直接写出m的值并分别求出S1与S2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 与双曲线y=
与双曲线y=  (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=  向上平移4个单位长度后,与y轴交于点C,与双曲线y=
向上平移4个单位长度后,与y轴交于点C,与双曲线y=  (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A.3
B.6
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数 yl= x ( x ≥0 ) ,
 ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3  时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .

-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段
频数
频率
50.5~60.5
16
0.08
60.5~70.5
40
0.2
70.5~80.5
50
0.25
80.5~90.5
m
0.35
90.5~100.5
24
n
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在平面直角坐标系xOy中,函数y=
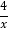 (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是6,求点P的坐标.

相关试题

