【题目】已知均是的函数，下表是与的几组对应值．

小聪根据学习函数的经验，利用上述表格所反映出的与之间的变化规律，分别对函数的图象与性质进行了探究．

下面是小聪的探究过程，请补充完整：

（1）如图，在同一平面直角坐标系中，描出上表中各组数值所对应的点，并画出函数的图象；

（2）结合画出的函数图象，解决问题：

①当时，对应的函数值约为_________；

②写出函数的一条性质：_________________________；

③当时，的取值范围是_________________________．

【答案】（1）描点作图见解析；（2）①3.13；②当时，有最小值；③，或．

【解析】

(1)根据给出的对应数值描点作图即可；(2)①根据图形观察可得答案，②根据图像得出性质即可，③观察图像利用函数值的大小确定自变量的取值范围即可．

解：描点作图如下：

（1）如图：

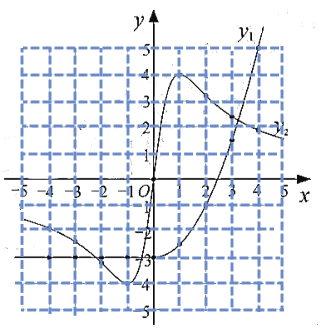
（2）观察图像得：①3.13；

②当时，有最小值；

③，或．

故答案为：当时，有最小值，，或．

关闭