【题目】如图，在平面直角坐标系中，抛物线经过、两点，与x轴交于另一点C，顶点为D．

求该抛物线的解析式及点C、D的坐标；

经过点B、D两点的直线与x轴交于点E，若点F是抛物线上一点，以A、B、E、F为顶点的四边形是平行四边形，求点F的坐标；

如图是抛物线上的点，Q是直线AP上方的抛物线上一动点，求的最大面积和此时Q点的坐标．

【答案】（1）；（2）；（3）当时，的最大面积为，

此时．

【解析】

（1）首先将点A、B的坐标代入抛物线的解析式中，即可求出待定系数的值．再通过配方、令函数值为0可求出顶点D以及点C的坐标．
（2）由图可知：若以A、B、E、F为顶点的四边形是平行四边形，令EF∥AB显然不符合要求，那么只需考虑BF∥AE即可，那么还需满足BF=AE；首先求出直线BD的解析式，进而得出点E的坐标以及AE、BF的长，由此可确定点F的坐标，再代入抛物线的解析式中验证即可．
（3）分别过点P、Q作x轴的垂线，那么△APQ的面积可由五边形和△APS（以解答图为准）的面积差求得，在得到关于△APQ的面积和Q点横坐标的函数关系式，根据函数的性质即可确定该题的答案．

解：抛物线经过、两点，有：

，

解得

抛物线的解析式为：

由，

解得：，

由

．

四边形AEBF是平行四边形，

设直线BD的解析式为：，则

，

，

解得

直线BD的解析式为：；

当时，

，，

，，

，

的横坐标为2，

，

．

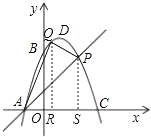
如图，设，作轴，轴于点S、R，且，

，，，，

当时，的最大面积为，

此时．

关闭