【题目】(10分)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
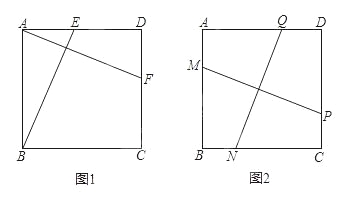
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
参考答案:
【答案】(1)证明:如图(1),在正方形ABCD中,AB=DA,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,
∵在△ABE和△DAF中, 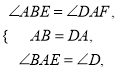
∴△ABE≌△DAF(ASA),∴BE=AF.
(2)解:MP与NQ相等.理由如下:
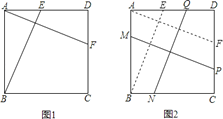
如图(2),过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则BE=NQ,AF=MP.只需证BE=AF即可.与(1)的情况完全相同.

【解析】试题分析:(1)要证明AF=BE成立,只需要根据条件证明△ABE≌△DAF即可;(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,将问题转化为证明AF=BE,即可应用(1)的结论.
试题解析:(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,
∴∠ABE=∠DAF,∵在△ABE和△DAF中,
 ,∴△ABE≌△DAF(ASA),∴AF=BE;
,∴△ABE≌△DAF(ASA),∴AF=BE;
(2)解:MP与NQ相等.
理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,
由(1)可知MP=NQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在100个数据中,用适当的方法,抽取50个作为样本进行统计,频数分布表中55~58这一组数据的频率是0.12,那么估计这100个数据中,落在55~58之间的约有( )
A. 120个 B. 60个 C. 12个 D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,参加跳高的15名运动员的成绩如下表所示:
成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
人数
1
2
4
3
3
2
这15名运动员跳高成绩的中位数是( )
A. 4 B. 1.70 C. 1.75 D. 1.65
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动.若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动,求:
(1)经过6秒后,BP= cm,BQ= cm;
(2)经过几秒后,△BPQ是直角三角形?
(3)经过几秒△BPQ的面积等于
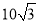 cm2?
cm2?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
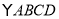 中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=
中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=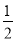 ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )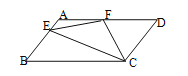
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】面试时,某人的基本知识、表达能力、工作态度的成绩分别是90分、80分、85分,若依次按20%、40%、40%的比例确定成绩,则这个人的面试成绩是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列多项式:a+b,2a-b2,3a+b3,4a-b4,…,按此规律第10个多项式是________.
相关试题

