【题目】已知二次函数的图像与y轴交于点A，一次函数的图像经过点A，且与二次函数图像的另一个交点为点B．

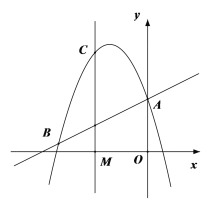
（1）用含有字母b代数式表示点B的坐标．

（2）点M的坐标为（－2，0），过点M作x轴的垂线交抛物线于点C．

①当x＜－2时，y1＜y2，求b的取值范围；

②若△ABC是直角三角形，求b的值．

【答案】（1）；（2）①，②b的值为-4或．

【解析】

（1）根据二次函数解析式可得A（0，2），代入可求出一次函数解析式，联立一次函数解析式和二次函数解析式成方程组，解方程组即可得出点B的坐标；

（2）①由函数图象得，当x＜时，y1＜y2，结合题意得出关于b的不等式，求解即可；②分别求出，和，由函数图象可得∠ABC不可能为90°，故分和两种情况，分别利用勾股定理得出方程求解即可．

解：（1）∵二次函数的图像与y轴交于点A，

∴A（0，2），

把A（0，2）代入得：，

∴一次函数解析式为：，

联立，解得：或，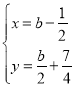

∴点B的坐标为；

（2）①点B的坐标为，

由函数图象得：当x＜时，y1＜y2，

由题意得：当x＜－2时，y1＜y2，

∴，

解得：；

②当x＝－2时，，

∴C（－2，－2b－2），

∵A（0，2），B，

∴，，，

由函数图象可得：∠ABC不可能为90°，

∴当时，AB2+AC2=BC2，

即，

解得：或（不合题意，舍去），

当时，AC2+BC2= AB2，

即，

解得：或（不合题意，舍去），

综上，b的值为－4或．

关闭