【题目】已知抛物线 y= ![]() x2﹣2x的顶点是A,与x轴相交于点B、C两点(点B在点C的左侧).
x2﹣2x的顶点是A,与x轴相交于点B、C两点(点B在点C的左侧).
(1)求A、B、C的坐标;
(2)直接写出当y<0时x的取值范围.
参考答案:
【答案】
(1)解:y= ![]() x2﹣2x=
x2﹣2x= ![]() (x2﹣4x+4)﹣2=
(x2﹣4x+4)﹣2= ![]() (x﹣2)2﹣2,
(x﹣2)2﹣2,
则函数的顶点坐标是(2,﹣2),
即A的坐标是(2,﹣2).
令y=0,则 ![]() x2﹣2x=0,
x2﹣2x=0,
解得x=0或4,
则B的坐标是(0,0),C的坐标是(4,0)
(2)解:x的范围是0<x<4.
【解析】(1)利用配方法即可确定函数的顶点坐标;令y=0,解方程即可求得与x轴的交点的横坐标;(2)y<0求x的范围,根据函数开口向上,以及函数与x轴的交点即可确定.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校的科技节比赛设置了如下项目:A—船模;B—航模;C—汽模.右图为该校参加科技比赛的学生人数统计图.
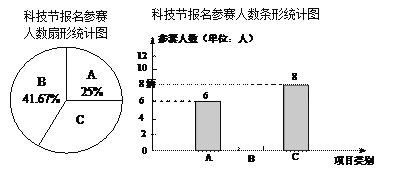
(1)该校报名参加B项目学生人数是 人;
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是 °;
(3)为确定参加区科技节的学生人选,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛,每人进行了4次试飞,对照一定的标准,判分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,你打算安排谁代表学校参赛?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )
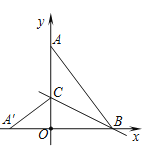
A. y=﹣
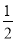 x+
x+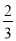 B. y=﹣x+
B. y=﹣x+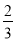 C. y=﹣
C. y=﹣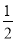 x+
x+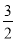 D. y=﹣2x+
D. y=﹣2x+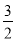
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2=x的根是( )
A.x=1
B.x=0
C.x1=0,x2=1
D.非以上答案 -
科目: 来源: 题型:
查看答案和解析>>【题目】若a是4的平方根,b=-42,那么a+b的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个还未画好的中心对称图形,它是一个四边形ABCD,其中A与C,B与D是对称点.
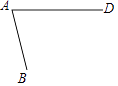
(1)用尺规作图先找出它的对称中心,再把这个四边形画完整;
(2)求证:四边形ABCD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2a3=a6
B.a3÷a2=a
C.(a3)2=a9
D.a2+a3=a5
相关试题

