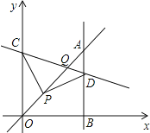
【题目】如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
A.(![]() ,
,![]() ) B.(3,3) C. (
) B.(3,3) C. (![]() ,
,![]() ) D.(
) D.(![]() ,
,![]() )
)
参考答案:
【答案】D
【解析】
试题分析:过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H, ∠CMP=∠DNP=∠CPD=90°,
∴∠MCP+∠CPM=90°,∠MPC+∠DPN=90°,
∴∠MCP=∠DPN,
∵P(1,1),
∴OM=BN=1,PM=1,
∴△MCP≌△NPD,
∴DN=PM,PN=CM,
∵BD=2AD,
∴设AD=x,BD=2x,
∵P(1,1),
∴DN=2x﹣1,
则2x﹣1=1,
解得:x=1,即BD=2,C的坐标是(0,3),
∵直线y=x,
∴AB=OB=3,
在Rt△DNP中,由勾股定理得:PC=PD=![]() 在Rt△MCP中,由勾股定理得:CM=2
在Rt△MCP中,由勾股定理得:CM=2
则C的坐标是(0,3),设直线CD的解析式是y=kx+3,
把D(3,2)代入得:k=﹣![]()
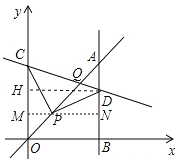
即直线CD的解析式是y=﹣![]() x+3, 即方程组为:
x+3, 即方程组为: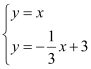
解得:![]() ,即Q的坐标是(
,即Q的坐标是(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=﹣6x+5的图象可由正比例函数______的图象向上平移5个单位长度得到.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在y=5x+a﹣2中,若y是x的正比例函数,则常数a=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l为x+y=8,点P(x,y)在l上且x>0,y>0,点A的坐标为(6,0).
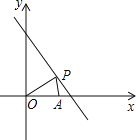
(1)设△OPA的面积为S,求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标;
(3)在直线l上有一点M,使OM+MA的和最小,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+4的图象经过点A(﹣3,﹣2).
(1)求这个一次函数的关系式;
(2)判断点B(﹣5,3)是否在这个函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,-3)所在的象限为( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面说法中正确的是( )
A.两个变量间的关系只能用关系式表示
B.图象不能直观的表示两个变量间的数量关系
C.借助表格可以表示出因变量随自变量的变化情况
D.以上说法都不对
相关试题

