【题目】如图,点A(0,8),点B(4,0),连接AB,点M,N分别是OA,AB的中点,在射线MN上有一动点P.若△ABP是直角三角形,则点P的坐标是__.
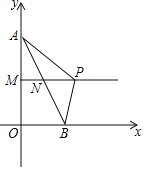
参考答案:
【答案】(2![]() +2,4)或(12,4).
+2,4)或(12,4).
【解析】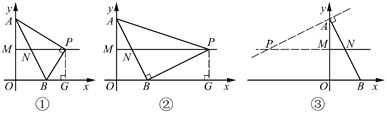
如图,∠APB=90°,∠ABP=90°,∠BAP=90°均可以使△ABP是直角三角形,故本题应该对这三种情况分别进行讨论.
(1) ∠APB=90°,如图①.
过点P作PG⊥OB,垂足为G.
∵点A的坐标为(0, 8),点B的坐标为(4, 0),
∴OA=8,OB=4.
∴在Rt△AOB中, ![]() .
.
∵点M,N分别是OA,AB的中点,
∴MN∥OB, ![]() ,
, ![]() .
.
∵MN∥OB,PG⊥OB,
∴PG=OM=4.
设PN=x,则MP=MN+PN=2+x,
∵OG=MP=2+x,
∴BG=OG-OB=2+x-4=x-2.
∵在Rt△AMP中,AP2=AM2+PM2=42+(2+x)2=16+(2+x)2,
在Rt△BGP中,BP2=BG2+PG2=(x-2)2+42=(x-2)2+16,
又∵在Rt△APB中,AB2=AP2+BP2,
∴16+(2+x)2+(x-2)2+16=![]() =80.
=80.
∴x=![]() ,即PN=
,即PN=![]() .
.
∵OG=2+x=![]() ,PG =4.
,PG =4.
∴点P的坐标为(![]() , 4).
, 4).
(2) ∠ABP=90°,如图②.
过点P作PG⊥OB,垂足为G.
设PN=x,则MP=OG=2+x,BG=x-2.
∵![]() ,AM=4,PG=4,
,AM=4,PG=4,
又∵在Rt△AMP中,AP2=16+(2+x)2,
在Rt△BGP中,BP2=(x-2)2+16,
∴在Rt△APB中,AB2=AP2-BP2=16+(2+x)2-[(x-2)2+16]= ![]() =80.
=80.
∴x=10即PN=10.
∵OG=2+x=2+10=12,PG=4.
∴点P的坐标为(12, 4).
(3) ∠BAP=90°,如图③.
由图③可以看出,在此种情况下点P不在射线MN上,不符合题意.
综上所述,点P的坐标为(![]() , 4)或(12, 4).
, 4)或(12, 4).
故本题应填写:(![]() , 4)或(12, 4).
, 4)或(12, 4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】“阅读让自己内心强大,勇敢面对抉择与挑战.”某校倡导学生读书,下面的表格是该校九年级学生本学期内阅读课外书籍情况统计表.请你根据统计表中提供的信息,求出表中a、b的值:a=_____,b=_____.
图书种类
频数
频率
科普常识
210
b
名人传记
204
0.34
中外名著
a
0.25
其他
36
0.06
-
科目: 来源: 题型:
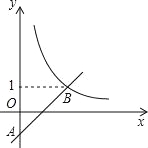
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数y=
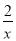 的图象相交于点B(m,1).
的图象相交于点B(m,1). (1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】辽宁男篮夺冠后,从4月21日至24日各类媒体关于“辽篮CBA夺冠”的相关文章达到81000篇,将数据81000用科学记数法表示为( )
A. 0.81×104B. 0.81×105C. 8.1×104D. 8.1×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的计算正确的是( )
A. a3a2=a6B. 5a﹣a=5C. (﹣a3)2=a6D. (a3)2=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
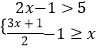 ,并在数轴上表示出不等式组的解集.
,并在数轴上表示出不等式组的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣2y=﹣3,则x﹣2y+5的值是( )
A.0
B.2
C.5
D.8
相关试题

