搜索
【题目】如图，反比例函数y=
（k≠0）与直线交于A，B两点．
（1）求证：OB=OA；
（2）连接CA交y轴于D点BD∥x轴，判断CB，CD的数量关系；
（3）求
的值．
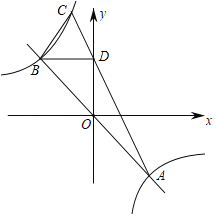
【答案】（1）见解析；（2）BC=CD；（3）
【解析】
（1）设A（a，
），又设AB的解析式为y=mx（m≠0），把A点坐标代入求得AB：y=
x，再联立方程组求得b点坐标，进而根据坐标特点得出A和B两点关于原点对称，便可得OA=OB；
（2）由AD坐标求得AD的解析式，再求得C点坐标，由两点距离公式求得BC与CD便可判断BC=CD；
（3）由两点距离公式求得CB与CA，再求比值便可．
（1）设A（a，），又设直线AB的解析式为y=mx（m≠0），则
，
∴m=，
∴AB：y=x，
联立方程组
，
解得，
，或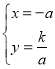
，
∴
，
∴点A与点B关于原点对称，
∴OA=OB；
（2）∵BD∥x轴，
∴D（0，﹣），
设直线AD的解析式为：y=nx﹣（n≠0），
代入A点坐标得，=an-，
∴
，
∴AD：y=
，
联立方程组
，
解得，，或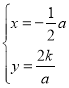
，
∴
，
∴
，
，
∴BC=CD；
（3）
，
∴
．
