【题目】如图,已知AB为⊙O的直径,AC为⊙O的切线,OC交⊙O于点D,BD的延长线交AC于点E.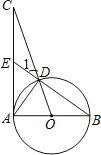
(1)求证:∠1=∠CAD;
(2)若AE=EC=2,求⊙O的半径.
参考答案:
【答案】
(1)
证明:∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠BDO=90°,
∵AC为⊙O的切线,
∴OA⊥AC,
∴∠OAD+∠CAD=90°,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠1=∠BDO,
∴∠1=∠CAD;
(2)
解:∵∠1=∠CAD,∠C=∠C,
∴△CAD∽△CDE,
∴CD:CA=CE:CD,
∴CD2=CACE,
∵AE=EC=2,
∴AC=AE+EC=4,
∴CD=2 ![]() ,
,
设⊙O的半径为x,则OA=OD=x,
则Rt△AOC中,OA2+AC2=OC2,
∴x2+42=(2 ![]() +x)2,
+x)2,
解得:x= ![]() .
.
∴⊙O的半径为 ![]()
【解析】(1)由AB为⊙O的直径,AC为⊙O的切线,易证得∠CAD=∠BDO,继而证得结论;(2)由(1)易证得△CAD∽△CDE,然后由相似三角形的对应边成比例,求得CD的长,再利用勾股定理,求得答案.此题考查了切线的性质、圆周角定理以及相似三角形的判定与性质.注意证得△CAD∽△CDE是解此题的关键.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,E、M在BC上,则∠EAM等于 ( )
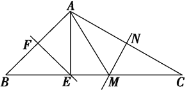
A. 58° B. 32°
C. 36° D. 34°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号
分组
频数
一
6≤m<7
2
二
7≤m<8
7
三
8≤m<9
a
四
9≤m≤10
2

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2 .
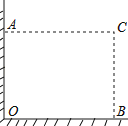
(1)求这地面矩形的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少? -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
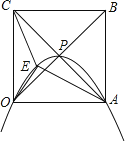
(1)建立适当的平面直角坐标系,
①直接写出O、P、A三点坐标;
②求抛物线L的解析式;
(2)求△OAE与△OCE面积之和的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是
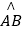 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 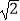 时,则阴影部分的面积为( )
时,则阴影部分的面积为( ) 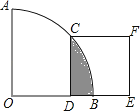
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
相关试题

