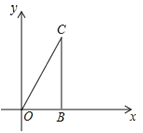
【题目】如图, ![]() 中是直角三角形,OB与
中是直角三角形,OB与![]() 轴正半轴重合,
轴正半轴重合, ![]() ,且OB=1,
,且OB=1, ![]() ,将
,将![]() 绕原点O逆时针旋转60°再将其各边扩大为原来的
绕原点O逆时针旋转60°再将其各边扩大为原来的![]() 倍,使
倍,使![]() ,得到
,得到![]() ,将
,将![]() 绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使
绕原点O逆时针旋转60°再将其各边扩大为原来的m倍,使![]() ,得到
,得到![]() ……,如此继续下去,得到
……,如此继续下去,得到![]() ,则m的值和点
,则m的值和点![]() 的坐标是 ( )
的坐标是 ( )
A. 2, ![]() B. 2,
B. 2, ![]()
C. ![]() ,
, ![]() D.
D. ![]() ,
, ![]()
参考答案:
【答案】A
【解析】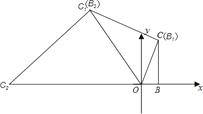
∵∠OBC=90°,OB=1,BC=![]() ,
,
∴tan∠BOC=![]() =
=![]() ,
,
∴∠BOC=60°,
∴OC=2OB=2×1=2,
∵将△OBC绕原点O逆时针旋转60再将其各边扩大为原来的m倍,使OB1=OC,
∴m=2,
∴OC1=2OC=2×2=4=22,
OC2=2OC1=2×4=8=23,
OC3=2OC2=2×8=16=24,
…,
OCn=2n+1,
∴OC2017=22018,
∵每一次的旋转角是60,
∴旋转6次是一个周期,
∵2017÷6=336…1,
∴点C2017与点C1在同一射线上,坐标为![]() .
.
故答案为:2, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是方程x2-m=0的解,则m=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益Z(元)会相应降低且Z与x之间也大致满足如图②所示的一次函数关系.
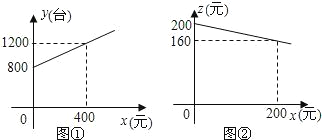
(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则3a________3b(填“<”、“=”或“>”号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(-x)x2(-x)6=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程中,有两个不相等实数根的是( )
A.3x2﹣5x﹣2=0B.a2+2a+3=0C.m2﹣4m+4=0D.y2+4=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆锥的底面积为9πcm2 , 母线长为6cm,则圆锥的侧面积是( )
A.18πcm2
B.27πcm2
C.18cm2
D.27cm2
相关试题

