【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
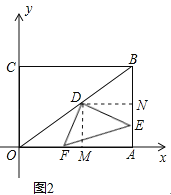
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
参考答案:
【答案】(1)3;(2)∠DEF的大小不变,tan∠DEF=![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题(1)当t=3时,点E为AB的中点,由三角形的中位线定理得出DE∥EA,DE=![]() OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
(2)作DM⊥OA于点M,DN⊥AB于N,证明四边形DMAN是矩形,得出∠MDN=90°,DM∥AB,DN∥OA,由平行线得出比例式![]() ,
,![]() ,由三角形中位线定理得出DM=
,由三角形中位线定理得出DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,证明ΔDMF∽ΔDNE,得出
OA=4,证明ΔDMF∽ΔDNE,得出![]() ,再由三角函数的定义即可得解;
,再由三角函数的定义即可得解;
(3)作DM⊥OA于M,DN⊥AB于N,若AD将ΔDEF的面积分为1:2的两部分,设AD交EF于点G,则点G为EF的三等分点.
①当点E到达中点之前时,NE=3-t,由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4+MF=
,求出AF=4+MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),求出直线AD的解析式为y=-
),求出直线AD的解析式为y=-![]() +6,把G(
+6,把G(![]() ,
,![]() )代入即可求出t的值;
)代入即可求出t的值;
②当点超过中点之后,NE=t-3,由由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4-MF=
,求出AF=4-MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),代入直线AD的解析式y=-
),代入直线AD的解析式y=-![]() +6即可求出t的值;
+6即可求出t的值;
试题解析: (1)当t=3时,点E为AB的中点,
∵A(8,0),C(0,6),
∴OA=8,OC=6,
∵点D为OB的中点,
∴DE∥OA,DE=![]() OA=4,
OA=4,
∵四边形OABC是矩形,
∴OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°,
∴四边形DFAE是矩形,
∴DF=AE=3;
(2)∠DEF的大小不变;理由如下:
作DM⊥OA于M,DN⊥AB于N,如图2所示:
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM∥AB,DN∥OA,
∴![]() ,
,![]() ,
,
∵点D为OB的中点,
∴M、N分别是OA、AB的中点,
∴DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,
OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN,
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE,
∴![]() ,
,
∵∠EDF=90°,
∴tan∠DEF=![]() ;
;
(3)作DM⊥OA于M,DN⊥AB于N,
若AD将△DEF的面积分成1:2的两部分,
设AD交EF于点G,则点G为EF的三等分点;
①当点E到达中点之前时,如图3所示,NE=3﹣t,

由△DMF∽△DNE得:MF=![]() (3﹣t),
(3﹣t),
∴AF=4+MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
设直线AD的解析式为y=kx+b,
把A(8,0),D(4,3)代入得:![]() ,
,
解得: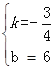 ,
,
∴直线AD的解析式为y=﹣![]() x+6,
x+6,
把G(![]() ,
,![]() )代入得:t=
)代入得:t=![]() ;
;
②当点E越过中点之后,如图4所示,NE=t﹣3,
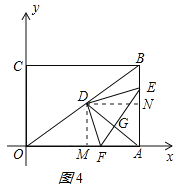
由△DMF∽△DNE得:MF=![]() (t﹣3),
(t﹣3),
∴AF=4﹣MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
代入直线AD的解析式y=﹣![]() x+6得:t=
x+6得:t=![]() ;
;
综上所述,当AD将△DEF分成的两部分的面积之比为1:2时,t的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如4=22﹣02,12=42﹣22,20=62﹣42,因此 4,12,20 都是“神秘数”,则下面哪个数是“神秘数”( )
A.56B.60C.62D.88
-
科目: 来源: 题型:
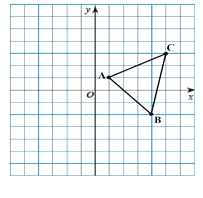
查看答案和解析>>【题目】如图,在平面直角坐标系中, ABC 三个顶点的坐标分别为 A(1,1) , B(4, 2) ,C (5, 3) .
(1)在图中画出 ABC 关于 y 轴的对称 图形 A1B1C1 ;(要求:画出三角形,标出相应顶点的 字母,不写结论)
(2)分别写出A1B1C1 三个顶点的坐标.
-
科目: 来源: 题型:
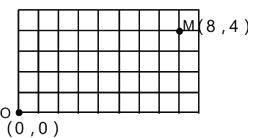
查看答案和解析>>【题目】四个点的坐标分别是: A(0, 3) 、 B(2, 4) 、 C(6, 2) 、 D(5, 0) .
(1)在下面的方格中分别作出 A 、 B 、 C 、 D 四个点的位置;
(2)顺次连结 A 、 B 、 C 、 D 四个点,得到四边形 ABCD ,求四边形 ABCD 的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来市政府每年出资新建一批廉租房,使城镇住房困难的居民住房状况得到改善.下面是某小区2006~2008年每年人口总数和人均住房面积的统计的折线图(人均住房面积=该小区住房总面积/该小区人口总数,单位:㎡/人).
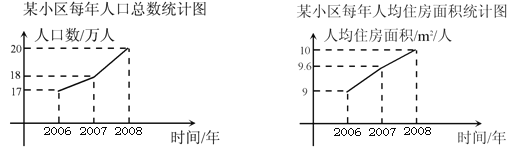
根据以上信息,则下列说法:①该小区2006~2008年这三年中,2008年住房总面积最大;②该小区2007年住房总面积达到1.728×106 m
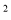 ;③该小区2008年人均住房面积的增长率为4%.其中正确的有
;③该小区2008年人均住房面积的增长率为4%.其中正确的有 (A)①②③(B)①②(C)① (D)③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2m+3的正方形纸片中剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,

(1)求拼接成的长方形面积.
(2)若拼成的长方形一边长为 m,求此长方形的周长.
-
科目: 来源: 题型:
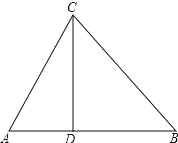
查看答案和解析>>【题目】某校要在一块三角形空地上种植花草,如图所示,AC=13 米、AB=14 米、BC=15 米, 若线段 CD 是一条引水渠,且点 D 在边 AB 上.已知水渠的造价每米 150 元.问:点 D 与点 C 距离多远时,水渠的造价最低?最低造价是多少元?
相关试题

