【题目】设抛物线的解析式为y=ax2 , 过点B1(1,0)作x轴的垂线,交抛物线于点A1(1,2);过点B2( ![]() ,0)作x轴的垂线,交抛物线于点A2;…;过点Bn((
,0)作x轴的垂线,交抛物线于点A2;…;过点Bn(( ![]() )n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
)n﹣1 , 0)(n为正整数)作x轴的垂线,交抛物线于点An , 连接AnBn+1 , 得Rt△AnBnBn+1 .
(1)求a的值;
(2)直接写出线段AnBn , BnBn+1的长(用含n的式子表示);
(3)在系列Rt△AnBnBn+1中,探究下列问题:
①当n为何值时,Rt△AnBnBn+1是等腰直角三角形?
②设1≤k<m≤n(k,m均为正整数),问:是否存在Rt△AkBkBk+1与Rt△AmBmBm+1相似?若存在,求出其相似比;若不存在,说明理由.
参考答案:
【答案】
(1)
解:∵点A1(1,2)在抛物线的解析式为y=ax2上,
∴a=2;
(2)
解:AnBn=2x2=2×[( ![]() )n﹣1]2=(
)n﹣1]2=( ![]() )2n-3,
)2n-3,
BnBn+1=( ![]() )n;
)n;
(3)
解:由Rt△AnBnBn+1是等腰直角三角形得AnBn=BnBn+1,则:( ![]() )2n-3=(
)2n-3=( ![]() )n,
)n,
2n﹣3=n,n=3,
∴当n=3时,Rt△AnBnBn+1是等腰直角三角形,
②依题意得,∠AkBkBk+1=∠AmBmBm+1=90°,
有两种情况:i)当Rt△AkBkBk+1∽Rt△AmBmBm+1时,
![]() =
= ![]() ,
,  =
= ![]() ,
, ![]() =
= ![]() ,
,
所以,k=m(舍去),
ii)当Rt△AkBkBk+1∽Rt△Bm+1BmAm时,
![]() =
= ![]() ,
,  =
=  ,
, ![]() =
= ![]() ,
,
∴k+m=6,
∵1≤k<m≤n(k,m均为正整数),
∴取 ![]() 或
或 ![]() ;
;
当 ![]() 时,Rt△A1B1B2∽Rt△B6B5A5,
时,Rt△A1B1B2∽Rt△B6B5A5,
相似比为: ![]() =
= ![]() =64,
=64,
当 ![]() 时,Rt△A2B2B3∽Rt△B5B4A4,
时,Rt△A2B2B3∽Rt△B5B4A4,
相似比为: ![]() =
= ![]() =8,
=8,
所以:存在Rt△AkBkBk+1与Rt△AmBmBm+1相似,其相似比为64:1或8:1.

【解析】本题考查了二次函数的综合问题,这是一个函数类的规律题,把坐标、二次函数和线段有机地结合在一起,以求线段的长为突破口,以相似三角形的对应边的比为等量关系,代入计算解决问题,综合性较强,因为本题小字标较多,容易出错.(1)直接把点A1的坐标代入y=ax2求出a的值;(2)由题意可知:A1B1是点A1的纵坐标:则A1B1=2×12=2;A2B2是点A2的纵坐标:则A2B2=2×( ![]() )2=
)2= ![]() ;…则AnBn=2x2=2×[(
;…则AnBn=2x2=2×[( ![]() )n﹣1]2=(
)n﹣1]2=( ![]() )2n-3;
)2n-3;
B1B2=1﹣ ![]() =
= ![]() ,B2B3=
,B2B3= ![]() ﹣(
﹣( ![]() )2 =
)2 = ![]() =(
=( ![]() )2 , …,BnBn+1=(
)2 , …,BnBn+1=( ![]() )n;(3)因为Rt△AkBkBk+1与Rt△AmBmBm+1是直角三角形,所以分两种情况讨论:根据(2)的结论代入所得的对应边的比列式,计算求出k与m的关系,并与1≤k<m≤n(k,m均为正整数)相结合,得出两种符合条件的值,分别代入两相似直角三角形计算相似比.
)n;(3)因为Rt△AkBkBk+1与Rt△AmBmBm+1是直角三角形,所以分两种情况讨论:根据(2)的结论代入所得的对应边的比列式,计算求出k与m的关系,并与1≤k<m≤n(k,m均为正整数)相结合,得出两种符合条件的值,分别代入两相似直角三角形计算相似比.
【考点精析】本题主要考查了二次函数的性质和相似三角形的判定的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人利用扑克牌玩“10点”游戏,游戏规则如下:
①将牌面数字作为“点数”,如红桃6的“点数”就是6(牌面点数与牌的花色无关);
②两人摸牌结束时,将所摸牌的“点数”相加,若“点数”之和小于或等于10,此时“点数”之和就是“最终点数”;若“点数”之和大于10,则“最终点数”是0;
③游戏结束前双方均不知道对方“点数”;
④判定游戏结果的依据是:“最终点数”大的一方获胜,“最终点数”相等时不分胜负.
现甲、乙均各自摸了两张牌,数字之和都是5,这时桌上还有四张背面朝上的扑克牌,牌面数字分别是4,5,6,7.
(1)若甲从桌上继续摸一张扑克牌,乙不再摸牌,则甲获胜的概率为;
(2)若甲先从桌上继续摸一张扑克牌,接着乙从剩下的扑克牌中摸出一张牌,然后双方不再摸牌.请用树状图或表格表示出这次摸牌后所有可能的结果,再列表呈现甲、乙的“最终点数”,并求乙获胜的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.

(1)当∠AOB=18°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9°≈0.1564,cos9°≈0.9877,sin18°≈0.3090,cos18°≈0.9511,可使用科学计算器) -
科目: 来源: 题型:
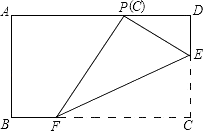
查看答案和解析>>【题目】如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E、F分别为边AD、BC的中点,对角线AC分别交BE,DF于点G、H.求证:AG=CH.

相关试题

