Question

【题目】（1）如图1，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数；

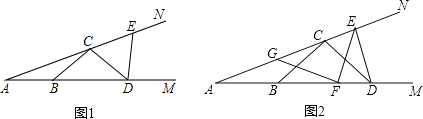
（2）如图2，点B、F、D在射线AM上，点G、C、E在射线AN上，且AB=BC=CD=DE=EF=FG=GA，求∠A的度数．

Answer 1

【答案】（1）∠A=21°；（2）∠A=；

【解析】

试题分析：（1）根据等边对等角可得∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，然后用∠A表示出∠EDM，计算即可求解；

（2）由特殊到一般，解题的思路与（1）相同．

解：（1）∵AB=BC=CD=DE，

∴∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，

根据三角形的外角性质，

∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，

又∵∠EDM=84°，

∴∠A+3∠A=84°，

解得，∠A=21°；

（2）∵AB=BC=CD=DE=EF=FG=GA，设∠A=x°，

则∠AFG=∠ACB=x°，∠CGF=∠CEF=∠CBF=∠CDF=2x°，

∠ECD=∠CED=∠EFD=∠EDF=3x°，

而∠A+∠CED+∠EDF=180°，故，即∠A=；