【题目】直线![]() 与
与![]() 交于
交于![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的度数为_____.
的度数为_____.
参考答案:
【答案】![]() 或
或![]()
【解析】
根据题意,分两种情况:(1)∠BOE是锐角;(2)∠BOE是钝角;然后根据垂线的性质,分类讨论,求出∠BOE的度数是多少即可.
(1)如图1,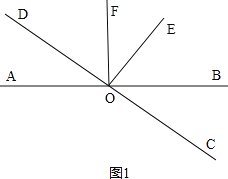 ,
,
∵直线OE⊥CD,
∴∠EOD=90°,
∵∠DOF=55°,
∴∠EOF=90°-55°=35°,
又∵直线OF⊥AB,
∴∠BOF=90°,
∴∠BOE=90°-35°=55°.
(2)如图2,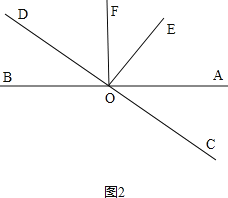 ,
,
∵直线OE⊥CD,
∴∠EOD=90°,
∵∠DOF=55°,
∴∠EOF=90°-55°=35°,
又∵直线OF⊥AB,
∴∠BOF=90°,
∴∠BOE=90°+35°=125°.
综上,可得∠BOE的度数是125°或55°.
故答案为:125°或55°.
-
科目: 来源: 题型:
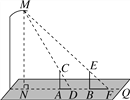
查看答案和解析>>【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为点G,连接CG,下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值
 ﹣1.其中正确的说法有( )个.
﹣1.其中正确的说法有( )个.
A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等式
 在实数范围内成立,其中a、x、y是两两不同的实数,则
在实数范围内成立,其中a、x、y是两两不同的实数,则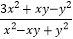 的值是( )
的值是( )A. 3 B.
 C. 2 D.
C. 2 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
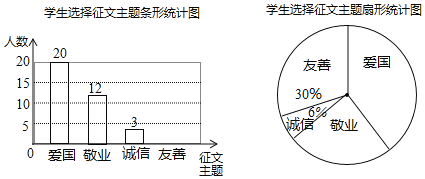
(1)将上面的条形统计图补充完整;
(2)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少度?
(3)如果该校七年级共有1200名考生,请估计选择以“友善”为主题的七年级学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)求二月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型每台进价为3500元,乙型每台进价为4000元,预计用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)对于(2)中刚进货的20台两种型号的手机,该店计划对甲型号手机在二月份售价基础上每售出一台甲型手机再返还顾客现金a元,乙型手机按销售价4400元销售,若要使(2)中所有方案获利相同,a应取何值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )

A. 4 B.
 C.
C.  D. 30
D. 30
相关试题

