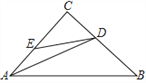
【题目】如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC=![]() (AB+AE);④ S△ADC=
(AB+AE);④ S△ADC=![]() S四边形ABDE,其中正确的结论个数为( )
S四边形ABDE,其中正确的结论个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】A
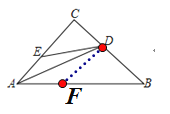
【解析】在AB上截取AF=AE,交AB于点F,如图所示:
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
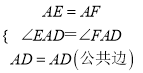 ,
,
∴△AED≌△AFD(SAS),
∴∠DEA=∠DFA,DF=DE,
又∵DE=DB,
∴DF=DB,
∴∠DFB=∠B,
又∵∠DFA+∠DFB=180o,∠DEA=∠DFA,
∴∠DEA+∠B=180°(等量代换),
又∵∠CED+∠AED=180o,
∴∠CED=∠B,
又∵∠C+∠CED+∠CDE=180o,∠C+∠CAB+∠B=180o,
∴∠CDE=∠CAB,
过点D作DG![]() AB于点G,如图所示:
AB于点G,如图所示:
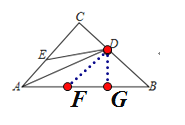
∵DG=DB(已证),
∴DG是BF的垂直平分线,
∴FG=BG,
∵AD是是∠CAB的角平分线,∠C=90°,DG![]() AB,
AB,
∴DC=DG,
在△ADC和△AGD中
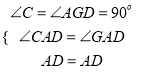 ,
,
∴△ADC≌△AGD(AAS),
∴AC=AG,
又∵AC=AE+CE,AG=AF+FG,
∴AE+CE=AF+FG,
又∵AE=AF,
∴CE=FG,
又∵FG=BG,
∴CE=BG,
∴AC=AE+BG,
又∵AB+AE=AG+BG+AE,AG=AC,
∴AB+AE=AC+AC=2AC,即AC=![]() (AB+AE),
(AB+AE),
∵S四边形ABDE=S△ABD+S△AED=![]() ,
,
∴S四边形ABDE ![]() ,
,
又∵S△ADC=![]() ,
,
∴S△ADC=![]() S四边形ABDE.
S四边形ABDE.
故①②③④都正确,共计4个正确.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂一月份的总产量为500吨,三月份的总产量达到为700吨.若平均每月增长率是x,则可以列方程( )
A.500(1+2x)=700
B.500(1+x2)=700
C.500(1+x)2=700
D.700(1+x2)=500 -
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹥0,则点P(-a,2)应在( )
A.第一象限B.第二象限C.第三象限D.第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①A、E、F、C在一条直线上,AE=CF,过E、F分别作DE⊥AC,B F⊥AC,若AB=CD.
(1)图①中有 对全等三角形,并把它们写出来.
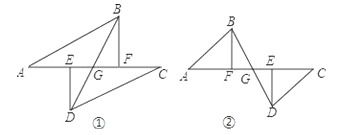
(2)求证:G是BD的中点.
(3)若将△ABF的边AF沿GA方向移动变为图②时,其余条件不变,第(2)题中的结论是否成立?如果成立,请予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正比例函数y=﹣3mx中,函数y的值随x值的增大而增大,则点A(m,3)在第_____象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成A,B,C,D四组,得到如下统计图:

(1)求A组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校8个班级进行足球友谊赛,比赛采用单循环赛制(参加比赛的队,每两队之间进行一场比赛),胜一场得3分,平一场得1分,负一场得0分,某班共得15分,并以不败成绩获得冠军,那么该班共胜场比赛.
相关试题

