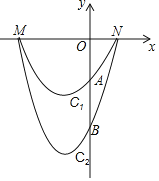
【题目】如图，抛物线C1与抛物线C2与x轴有相同的交点M，N（点M在点N的左侧），与x轴的交点分别为A，B，且点A的坐标为（0，﹣3），抛物线C2的解析式为y＝mx2+4mx﹣12m（m＞0）．

（1）求M，N两点的坐标；

（2）在第三象限内的抛物线C1上是否存在一点P，使得△PAM的面积最大，若存在，求出△PAM的面积的最大值；若不存在，说明理由；

（3）设抛物线C2的顶点为点D，顺次连接A，D，B，N，若四边形ADBN是平行四边形，求m的值．

【答案】（1）M（﹣6，0），N（2，0），（2）a＝﹣3时，△PAM的面积最大，面积的最大值是；（3）

【解析】

（1）令y＝0代入y＝mx2+4mx﹣12m，即可求出M、N两点的坐标；

（2）利用点A、M、N的坐标即可求出抛物线C1的解析式，再求出直线MA的解析式，然后设P的横坐标为a，过点P作PE∥y轴交MA于点E，所以△PAM的面积为PEOM，列出△PAM的面积与a的函数关系式，利用二次函数的性质即可求出△PAM的面积最大值；

（3）当AN∥DB时，求出m的值，此时只需要证明AN＝DB即可．

解：（1）令y＝0代入y＝mx2+4mx﹣12m，

∴0＝mx2+4mx﹣12m，

∴x＝2或x＝﹣6，

∴N（2，0），M（﹣6，0）；

（2）设抛物线C1的解析式为y＝a（x﹣2）（x+6），

把C（0，﹣3）代入y＝a（x﹣2）（x+6），

∴﹣3＝﹣12a，

∴，

∴抛物线的解析式为y＝，

设直线AM的解析式为y＝kx+b，

把M（﹣6，0）和A（0，﹣3）代入y＝kx+b，

∴，

∴，

∴直线AM的解析式为y＝﹣x﹣3，

设P的坐标为（a，a2+a﹣3），其中﹣6＜a＜0，

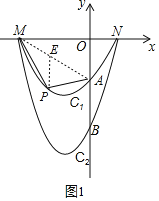
过点P作PE∥y轴交MA于点E，如图1，

∴，

∴＝，

∴==，

∴a＝﹣3时，△PAM的面积最大，面积的最大值是．

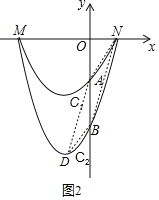
（3）如图2，由（1）可知：N（2，0），A（0，﹣3），

∴由勾股定理可知：AN＝，

求得直线AN的解析式为，

∴令x＝0代入y＝mx2+4mx﹣12m，

∴y＝﹣12m，

∴B（0，﹣12m），

由抛物线C2的解析式可知：D（﹣2，﹣16m），

若四边形ADBN是平行四边形，

∴AN∥BD，

设直线DB的解析式为，

∴﹣16m＝﹣3﹣12m，

∴，

∴B（0，9），D（﹣2，12），

∴，

∴AN＝BD，

∴时，四边形ADBN是平行四边形．

关闭