【题目】如图1,四根长度一定的木条,其中AB=6cm,CD=15cm,将这四根木条用小钉绞合在一起,构成一个四边形ABCD(在A、B、C、D四点处是可以活动的).现固定AB边不动,转动这个四边形,使它的形状改变,在转动的过程中有以下两个特殊位置.
位置一:当点D在BA的延长线上时,点C在线段AD上(如图2);
位置二:当点C在AB的延长线上时,∠C=90°.
(1)在图2中,若设BC的长为![]() ,请用含
,请用含![]() 的代数式表示AD的长;
的代数式表示AD的长;
(2)在图3中画出位置二的示意图
(3)利用图2、图3求图1的四边形ABCD中BC、AD边的长度.


参考答案:
【答案】(1)x+9;(2)见解析;(3)30,39.
【解析】
(1)根据旋转不变量在图2中表示出AD的长即可;(2)根据图形的旋转的性质作出图形即可;(3)根据题目中的所求表示出AD的长,利用勾股定理得到关于x的方程解得x的值即可.
(1)∵在四边形ABCD的转动过程中,BC、AD边的长度始终保持不变,BC=x,
∴在图2中,AC=BCAB=x6,AD=AC+CD=x+9.
(2)∴位置二的图见图3.
(3)∵在四边形ABCD转动的过程中,BC、AD边的长度始终保持不变,
∴在图3中,BC=x,AC=AB+BC=6+x,AD=x+9,
∵图3中,△ACD为直角三角形,∠C=90,
由勾股定理得:AC2+CD2=AD2,
∴(6+x)2+152=(x+9)2,
整理,得6x=180,
解得x=30,
即BC=30,
∴AD=39.
-
科目: 来源: 题型:
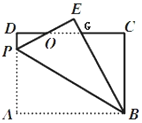
查看答案和解析>>【题目】如图, 矩形ABCD中,AB=8,BC=6,P为AD上一点, 将△ABP 沿BP翻折至△EBP, PE与CD相交于点O,BE与DC相交于G点,且OE=OD,
(1)求证:AP=DG
(2)若设AP=x,则GE=______,GC=_______(用含有x的代数式表示);并求AP的长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )

A.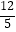
B.4
C.
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论: ①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2 ,
其中正确的结论有( )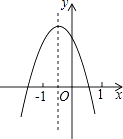
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
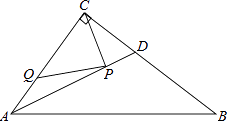
A.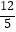
B.4
C.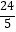
D.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论: ①abc<0;②b2﹣4ac>0;③3a+c>0;④(a+c)2<b2 ,
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
相关试题

