【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.

(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA= .
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=30°,则∠OGA= .
∠BAD,∠OBA=30°,则∠OGA= .
(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)
参考答案:
【答案】(1)15°;(2)10°;(3)![]() α;(4)
α;(4)![]() α+15°或
α+15°或![]() α-15°.
α-15°.
【解析】
试题分析:(1)由于∠BAD=∠ABO+∠BOA=α+90°,由AF平分∠BAD得到∠FAD=![]() ∠BAD,而∠FAD=∠EOD+∠OGA,2×45°+2∠OGA=α+90°,则∠OGA=
∠BAD,而∠FAD=∠EOD+∠OGA,2×45°+2∠OGA=α+90°,则∠OGA=![]() α,然后把α=30°代入计算即可;
α,然后把α=30°代入计算即可;
(2)由于∠GOA=![]() ∠BOA=30°,∠GAD=
∠BOA=30°,∠GAD=![]() ∠BAD,∠OBA=α,根据∠FAD=∠EOD+∠OGA得到3×30°+3∠OGA=α+90°,则∠OGA=
∠BAD,∠OBA=α,根据∠FAD=∠EOD+∠OGA得到3×30°+3∠OGA=α+90°,则∠OGA=![]() α,然后把α=30°代入计算;
α,然后把α=30°代入计算;
(3)由(2)得到∠OGA=![]() α;
α;
(4)讨论:当∠EOD:∠COE=1:2时,利用∠BAD=∠ABO+∠BOA=α+90°,∠FAD=∠EOD+∠OGA得到2×30°+2∠OGA=α+90°,则∠OGA=![]() α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,同理得∠OGA=![]() α-15°.
α-15°.
试题解析:(1)15°;
(2)10°;
(3)![]() α;
α;
(4)当∠EOD:∠COE=1:2时,
则∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=α+90°,
而AF平分∠BAD,
∴∠FAD=![]() ∠BAD,
∠BAD,
∵∠FAD=∠EOD+∠OGA,
∴2×30°+2∠OGA=α+90°,
∴∠OGA=![]() α+15°;
α+15°;
当∠EOD:∠COE=2:1时,则∠EOD=60°,
同理得到∠OGA=![]() α-15°,
α-15°,
即∠OGA的度数为![]() α+15°或
α+15°或![]() α-15°.
α-15°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A.两点之间,线段最短B.同旁内角互补
C.直角的补角仍然是直角D.垂线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
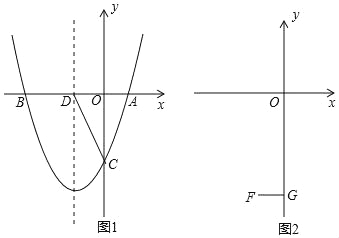
(1)若m=﹣3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在对称轴左侧的抛物线上有一点E,使S△ACE=
 S△ACD,求点E的坐标;
S△ACD,求点E的坐标;(3)如图2,设F(﹣1,﹣4),FG⊥y于G,在线段OG上是否存在点P,使∠OBP=∠FPG?若存在,求m的取值范围;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】会议室2排3号记作(2,3),那么3排2号记作( )
A.(3,2)B.(2,3)C.(-3,-2)D.(-2,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中正确的是( )
A.2a3a4=2a7
B.2(a+1)=2a+1
C.(2a4)3=8a7
D.a8÷a2=a4 -
科目: 来源: 题型:
查看答案和解析>>【题目】庆祝新中国成立70周年,国庆假期期间,各旅游景区节庆氛围浓厚,某景区同步设置的“我为祖国点赞”装置共收集约6390000个“赞”,这个数字用科学记数法可表示为( )
A.6.39×106B.0.639×106C.0.639×105D.6.39×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二元一次方程y﹣2x=1,用含x的代数式表示y,则y=_____.
相关试题

