【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表. 

(1)在图1中,“7分”所在扇形的圆心角等于°.
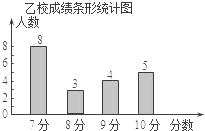
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
参考答案:
【答案】
(1)144
(2)解:利用扇形图:10分所占的百分比是90°÷360°=25%,
则总人数为:5÷25%=20(人),
得8分的人数为:20× ![]() =3(人).
=3(人).
如图
(3)解:根据乙校的总人数,知甲校得9分的人数是20﹣8﹣11=1(人).
甲校的平均分:(7×11+9+80)÷20=8.3分;
中位数为7分.
由于两校平均分相等,乙校成绩的中位数大于甲
校的中位数,所以从平均分和中位数角度上判断,
乙校的成绩较好
(4)解:因为选8名学生参加市级口语团体赛,甲校得
(10分)的有8人,而乙校得(10分)的只有5人,所以应选甲校.
【解析】解:(1)利用扇形图可以得出: “7分”所在扇形的圆心角=360°﹣90°﹣72°﹣54°=144°;
(1)根据扇形统计图中所标的圆心角的度数进行计算;(2)根据10分所占的百分比是90°÷360°=25%计算总人数,再进一步求得8分的人数,即可补全条形统计图;(3)根据乙校人数得到甲校人数,再进一步求得其9分的人数,从而求得平均数和中位数,并进行综合分析;(4)观察两校的高分人数进行分析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,分别以AB、BC、DC为边向外作正方形,它们的面积分别为S1、S2、S3.若S2=48,S3=9,则S1的值为( )
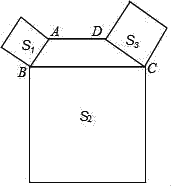
A. 18 B. 12 C. 9 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,D是边BC上的一点,已知AC=5,AD=6,BD=10,CD=5,那么三角形ABC的面积是( )
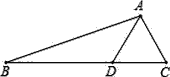
A. 30 B. 36 C. 72 D. 125
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简
(1)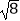 +|﹣2|﹣4sin45°﹣(
+|﹣2|﹣4sin45°﹣(  )﹣1
)﹣1
(2)解方程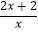 ﹣
﹣ 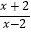 =
= 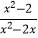 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理a2+b2=c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4,5),(5,12,13),(7,24,25),….分析上面勾股数组可以发现,4=1×(3+1),12=2×(5+1),24=3×(7+1),…分析上面规律,第5个勾股数组为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.

-
科目: 来源: 题型:
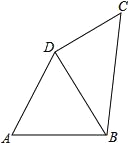
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
相关试题

