搜索
【题目】广州中学在“读书日”期间购进一批图书，需要用大小两种规格的纸箱来装运。2个大纸箱和3个小纸箱一次可以装155本书，5个大纸箱和6个小纸箱一次可以装350本书.
（1）一个大纸箱和一个小纸箱分别可以装多少本书？
（2）如果一共购入800本书，分别需要用多少个大，小纸箱？请直接写出所有装书方案（两种纸箱都需要用）
参考答案：
【答案】（1）大纸箱：40本. 小纸箱：25本；（2）方案一：大纸箱15个，小纸箱8个；方案一：大纸箱10个，小纸箱16个；方案一：大纸箱5个，小纸箱24个.
【解析】
（1）设一个大纸箱可以装x本书,一个小纸箱分别可以装y本书,根据2个大纸箱和3个小纸箱一次可以装155本书，5个大纸箱和6个小纸箱一次可以装350本书列方程组求解即可；
（2）设需a个大纸箱，b个小纸箱，根据一共购入800本书列二元一次方程求解即可.
（1）设一个大纸箱可以装x本书,一个小纸箱分别可以装y本书,由题意得
，
解之得
，
∴ 一个大纸箱可以装40本书,一个小纸箱分别可以装25本书；
（2）设需a个大纸箱，b个小纸箱，由题意得
40a+25b=800,
∵a，b是正整数，
∴
，
，
，
∴方案一：大纸箱15个，小纸箱8个；方案一：大纸箱10个，小纸箱16个；方案一：大纸箱5个，小纸箱24个.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为2，求图中阴影部分的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．
（1）观察猜想
如图1，当点D在线段BC上时，
①BC与CF的位置关系为： ．
②BC，CD，CF之间的数量关系为： ；（将结论直接写在横线上）
（2）数学思考
如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．
（3）拓展延伸
如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2
，CD=
BC，请求出GE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+2x﹣3与x轴交于A、B两点，且B（1，0）
（1）求抛物线的解析式和点A的坐标；
（2）如图1，点P是直线y=x上的动点，当直线y=x平分∠APB时，求点P的坐标；
（3）如图2，已知直线y=
x﹣
分别与x轴、y轴交于C、F两点，点Q是直线CF下方的抛物线上的一个动点，过点Q作y轴的平行线，交直线CF于点D，点E在线段CD的延长线上，连接QE．问：以QD为腰的等腰△QDE的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．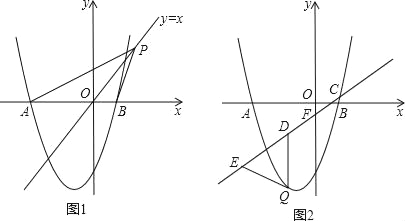
-
科目： 来源： 题型：
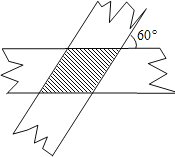
查看答案和解析>>【题目】如图，小华剪了两条宽为3的纸条，交叉叠放在一起，且它们较小的交角为60°，则它们重叠部分的面积为______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB∥CD∥EF，CD交AF于G，
（1）如图1，若CF平分∠AFE，∠A=70°，求∠C；
（2）如图2，请写出∠A，∠C和∠AFC的数量关系并说明理由.
-
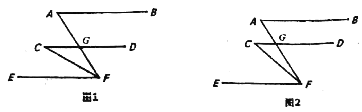
科目： 来源： 题型：
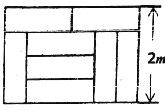
查看答案和解析>>【题目】如图,8块相同的小长方形地砖拼成一个大长方形,
（1）每块小长方形地砖的长和宽分别是多少?(要求列方程组进行解答)
（2）小明想用一块面积为7平方米的正方形桌布，沿着边的方向裁剪出一块新的长方形桌布，用来盖住这块长方形木桌，你帮小明算一算，他能剪出符合要求的桌布吗？
相关试题
