Question

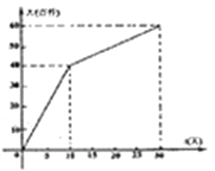
【题目】我市雷雷服饰有限公司生产了一款夏季服装，通过实验商店和网上商店两种途径进行销售，销售一段时间后，该公司对这种商品的销售情况，进行了为期30天的跟踪调查，其中实体商店的日销售量（百件）与时间（为整数，单位：天）的部分对应值如下表所示；网上商店的日销售量（百件）与时间（为整数，单位：天）的关系如下图所示.

时间 （天）	0	5	10	15	20	25	30
日销售量 （百件）	0	25	40	45	40	25	0

（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映与 的变化规律，并求出与的函数关系式及自变量的取值范围；

（2）求与的函数关系式，并写出自变量的取值范围；

（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为（百件），求与的函数关系式；当为何值时，日销售总量达到最大，并求出此时的最大值.

Answer 1

【答案】（1）y1=﹣t2+6t（0≤t≤30，且为整数）；（2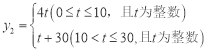）；（3）当0≤t≤10时，y=t2+6t+4t；当10＜t≤30时，y=t2+6t+t+30.当t=17或18时，y最大=91.2（百件）.

【解析】

试题分析：（1）根据观察可设y1=at2+bt+c，将（0，0），（5，25），（10，40）代入即可得到结论；

（2）当0≤t≤10时，设y2=kt，求得y2与t的函数关系式为：y2=4t，当10≤t≤30时，设y2=mt+n，将（10，40），（30，60）代入得到y2与t的函数关系式为：y2=k+30，

（3）依题意得y=y1+y2，当0≤t≤10时，得到y最大=80；当10＜t≤30时，得到y最大=91.2，于是得到结论．

试题解析：（1）根据观察可设y1=at2+bt+c，将（0，0），（5，25），（10，40）代入得：

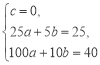，解得，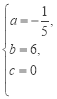

∴y1与t的函数关系式为：y1=﹣t2+6t（0≤t≤30，且为整数）；

（2）当0≤t≤10时，设y2=kt，

∵（10，40）在其图象上，∴10k=40，∴k=4，

∴y2与t的函数关系式为：y2=4t，

当10≤t≤30时，设y2=mt+n，

将（10，40），（30，60）代入得，解得，

∴y2与t的函数关系式为：y2=t+30，

综上所述，；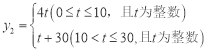

（3）依题意得y=y1+y2，当0≤t≤10时，y=t2+6t+4t=t2+10t=（t﹣25）2+125，

∴t=10时，y最大=80；

当10＜t≤30时，y=t2+6t+t+30=t2+7t+30=（t﹣）2+，

∵t为整数，∴t=17或18时，y最大=91.2，

∵91.2＞80，∴当t=17或18时，y最大=91.2（百件）．