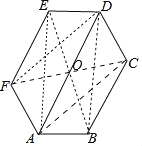
【题目】如图,六边形![]() 的内角都相等,
的内角都相等,![]() ,则下列结论成立的个数是
,则下列结论成立的个数是
①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形;⑤六边形
是平行四边形;⑤六边形![]() 即是中心对称图形,又是轴对称图形( )
即是中心对称图形,又是轴对称图形( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】
【解析】
试题分析:∵六边形ABCDEF的内角都相等,∴∠EFA=∠FED=∠FAB=∠ABC=120°,
∵∠DAB=60°,∴∠DAF=60°,∴∠EFA+∠DAF=180°,∠DAB+∠ABC=180°,
∴AD∥EF∥CB,故②正确,
∴∠FED+∠EDA=180°,∴∠EDA=∠ADC=60°,∴∠EDA=∠DAB,∴AB∥DE,故①正确,
∵∠FAD=∠EDA,∠CDA=∠BAD,EF∥AD∥BC,∴四边形EFAD,四边形BCDA是等腰梯形,
∴AF=DE,AB=CD,∵AB=DE,∴AF=CD,故③正确,
连接CF与AD交于点O,连接DF、AC、AE、DB、BE.
∵∠CDA=∠DAF,∴AF∥CD,AF=CD,∴四边形AFDC是平行四边形,故④正确,
同法可证四边形AEDB是平行四边形,∴AD与CF,AD与BE互相平分,∴OF=OC,OE=OB,OA=OD,
∴六边形ABCDEF既是中心对称图形,故⑤正确,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线
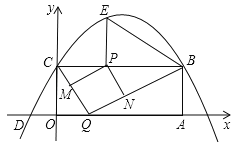
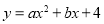 过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的标价为150元,若以8折降价出售.相对于进价仍获利20%,则该商品的进价为( )
A.120元
B.110元
C.100元
D.90元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧
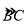 的长l.
的长l.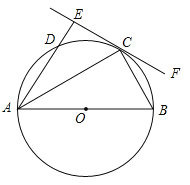
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列现象属于平移的是()
A.投篮时的篮球运动B.随风飘动的树叶在空中的运动
C.刹车时汽车在地面上的滑动D.冷水加热过程中小气泡变成大气泡
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知一次函数y=﹣2x+1,若﹣1≤x≤2,则y的取值范围为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程3x+y=7的正整数解有( )组.
A.0
B.1
C.2
D.无数
相关试题

