搜索
【题目】如图，边长为2a的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（ ）
A．
B．
C．
D．
参考答案：
【答案】A
【解析】
试题分析：取BC的中点G，连接MG，
∵旋转角为60°，∴∠MBH+∠HBN=60°，又∵∠MBH+∠MBC=∠ABC=60°，∴∠HBN=∠GBM，∵CH是等边△ABC的对称轴，∴HB=
AB，∴HB=BG，又∵MB旋转到BN，∴BM=BN，在△MBG和△NBH中，BG=BH,∠MBG=∠NBH，MB=NB，∴△MBG≌△NBH（SAS），∴MG=NH，根据垂线段最短，MG⊥CH时，MG最短，即HN最短，此时∵∠BCH=×60°=30°，CG=AB=×2a=a，∴MG=CG=×a=a，∴HN=a，故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中错误的命题是（ ）
A. （﹣3）2的平方根是±3
B. 平行四边形是中心对称图形
C. 单项式5x2y与﹣5xy2是同类项
D. 近似数3.14×103有三个有效数字
-
科目： 来源： 题型：
查看答案和解析>>【题目】设a,b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a,b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”．如函数
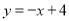，当x=1时，y=3；当x=3时，y=1，即当
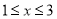时，有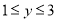
，所以说函数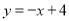是闭区间[1,3]上的“闭函数”．（1）反比例函数y=
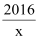是闭区间[1,2016]上的“闭函数”吗？请判断并说明理由；（2）若二次函数y=
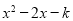是闭区间[1,2]上的“闭函数”，求k的值；（3）若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”，求此函数的表达式（用含m，n的代数式表示）．
-
科目： 来源： 题型：
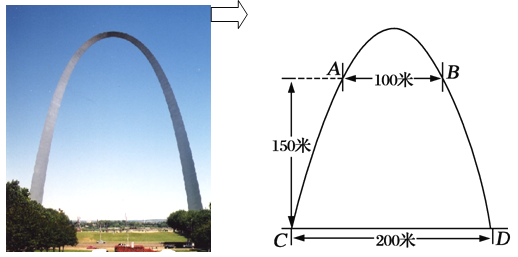
查看答案和解析>>【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物，是美国最高的独自挺立的纪念碑，如图．拱门的地面宽度为200米，两侧距地面高150米处各有一个观光窗，两窗的水平距离为100米，求拱门的最大高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
甲
乙
丙
丁
平均数（cm）
180
185
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（ ）
A. 甲 B. 乙 C. 丙 D. 丁
-
科目： 来源： 题型：
查看答案和解析>>【题目】将二次函数y=2（x﹣1）2﹣3的图象向右平移3个单位，则平移后的二次函数的顶点是（ ）
A. （﹣2，﹣3） B. （4，3） C. （4，﹣3） D. （1，0）
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中，是真命题的是
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线相等的四边形是矩形
C. 两条对角线互相垂直的四边形是菱形
D. 两条对角线互相垂直且相等的四边形是正方形
相关试题
