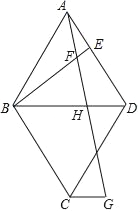
【题目】如图，菱形ABCD中，∠BAD＝60°，点E在边AD上，连接BE，在BE上取点F，连接AF并延长交BD于H，且∠AFE＝60°，过C作CG∥BD，直线CG、AF交于G．

(1)求证：∠FAE＝∠EBA；

(2)求证：AH＝BE；

(3)若AE＝3，BH＝5，求线段FG的长．

【答案】(1)证明见解析；(2)证明见解析；(3)FG＝．

【解析】

（1）先证明两三角形相似，再根据性质得到结果（2）先证明两三角形相似，再根据性质得到边的关系（3）先作辅助线，再证明两三角形相似，再根据相似三角形性质得到结果.

解：(1)∵∠AFE＝∠BAE＝60°、∠AEF＝∠BEA，

∴△AEF∽△BEA，

∴∠FAE＝∠ABE；

(2)∵四边形ABCD是菱形，且∠BAD＝60°，

∴AB＝AD、∠BAE＝∠ADB＝60°，

在△ABE和△DAH中，

∵

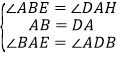
∴△ABE≌△DAH(ASA)，

∴AH＝BE；

(3)如图，连接AC交BD于点P，则AC⊥BD，且AC平分BD，

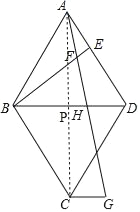
∵△ABE≌△DAH，

∴AE＝DH＝3，

则BD＝BH+DH＝8，

∴BP＝PD＝4，PH＝BH﹣BP＝1，

∵AB＝BD＝8，

∴AP＝＝4，

则AC＝2AP＝8，

∵CG∥BD，且P为AC中点，

∴∠ACG＝90°，CG＝2PH＝2，

∴AG＝＝14，BE＝AH＝AG＝7，

∵△AEF∽△BEA，

∴＝，即＝，

解得：AF＝，

∴FG＝AG﹣AF＝14﹣＝．

关闭