搜索
【题目】把一枚六个面编号为1，2，3，4，5，6的质地均匀的正六面体骰子连续投掷2次，若两次正面朝上的编号分别为m、n，则二次函数y=x2+mx+2n的图象与x轴至少有一个交点的概率是_____．
参考答案：
【答案】
【解析】
本题可先列出出现的点数的情况，因为二次图象开口向上，要使图象与x轴有至少有一个交点，则m2-8n≥0，再把m、n的值一一代入检验，看是否满足．最后把满足的个数除以掷骰子可能出现的点数的总个数即可．
掷骰子有6×6=36种情况。
根据题意有：m28n≥0，
因此满足的点有：n=1，m=3，4，5，6，
n=2，m=4，5，6，
n=3，m=5，6，
n=4，m=6，
n=5，m不存在，
n=6，m不存在，
共有10种，
故概率为：
=.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）已知长方体的长、宽、高分别是3x﹣4、2x和x，则它的表面积是_____；
（2）若3x3﹣x＝1，则9x4+12x3﹣3x2﹣7x+2018＝_____；
（3）若25x＝2000，80y＝2000，则
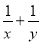的值为_____． -
科目： 来源： 题型：
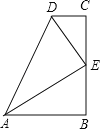
查看答案和解析>>【题目】如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC．
（1）求证：AE平分∠DAB；
（2）若AD＝8，BC＝6，求四边形ABCD的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂以每千克200元的价格购进甲种原料360千克，用于生产A、B两种产品，生产1件A产品或1件B产品所需甲、乙两种原料的千克数如下表：
产品/原料
A
B
甲（千克）
9
4
乙（千克）
3
10
乙种原料的价格为每千克300元，A产品每件售价3000元，B产品每件售价4200元，现将甲种原料全部用完，设生产A产品x件，B产品m件，公司获得的总利润为y元．
（1）写出m与x的关系式；
（2）求y与x的关系式；
（3）若使用乙种原料不超过510千克，生产A种产品多少件时，公司获利最大？最大利润为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】今年某市为创评“全国文明城市”称号，周末团市委组织志愿者进行宣传活动．班主任梁老师决定从4名女班干部（小悦、小惠、小艳和小倩）中通过抽签方式确定2名女生去参加．抽签规则：将4名女班干部姓名分别写在4张完全相同的卡片正面，把四张卡片背面朝上，洗匀后放在桌面上，梁老师先从中随机抽取一张卡片，记下姓名，再从剩余的3张卡片中随机抽取第二张，记下姓名．
（1）该班男生“小刚被抽中”是 事件，“小悦被抽中”是 事件（填“不可能”或“必然”或“随机”）；第一次抽取卡片“小悦被抽中”的概率为 ；
（2）试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出“小惠被抽中”的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABD和△ACE中，AB＝AD，AC＝AE，∠DAB＝∠CAE＝α，连接DC、BE．
（1）如图1，求证：DC＝BE；
（2）如图2，DC，BE交于点F，用含α的式子表示∠AFE；
（3）如图3，过A作AG⊥DC于点G，式于
的值为 ．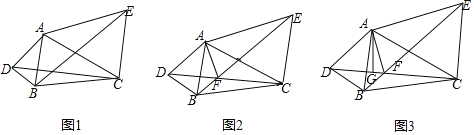
-
科目： 来源： 题型：
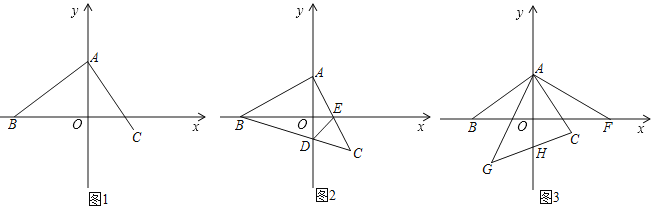
查看答案和解析>>【题目】如图，点A（0，2）在y轴上，点B在x轴上，作∠BAC＝90°，并使AB＝AC．
（1）如图1，若点B的坐标为（﹣3，0），求点C的坐标．
（2）如图2，若点B的坐标为（﹣4，0），连接BC交y轴于点D，AC交x轴于点E，连接DE，求证：BE＝AD+DE．
（3）在（1）的条件下，如图3，F为（4，0），作∠FAG＝90°，并使AF＝AG，连接GC交y轴于点H，求点H的坐标．
相关试题
