搜索
【题目】如图，点M、N分别是正五边形ABCDE的边BC、CD上的点，且BM=CN，AM交BN于点P． 
（1）求证：△ABM≌△BCN；
（2）求∠APN的度数．
参考答案：
【答案】
（1）证明：∵正五边形ABCDE，
∴AB=BC，∠ABM=∠C，
∴在△ABM和△BCN中
，
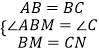∴△ABM≌△BCN（SAS）
（2）解：∵△ABM≌△BCN，
∴∠BAM=∠CBN，
∵∠BAM+∠ABP=∠APN，
∴∠CBN+∠ABP=∠APN=∠ABC= 
=108°．
即∠APN的度数为108°．
【解析】（1）利用正五边形的性质得出AB=BC，∠ABM=∠C，再利用全等三角形的判定得出即可；（2）利用全等三角形的性质得出∠BAM+∠ABP=∠APN，进而得出∠CBN+∠ABP=∠APN=∠ABC即可得出答案．
【考点精析】通过灵活运用多边形内角与外角，掌握多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°即可以解答此题．
-
科目： 来源： 题型：
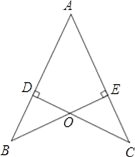
查看答案和解析>>【题目】如图，AB=AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．
（1）求证：AD=AE；
（2）连接OA，BC，试判断直线OA，BC的关系并说明理由．
-
科目： 来源： 题型：
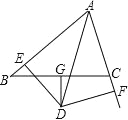
查看答案和解析>>【题目】如图，G 为 BC 的中点，且 DG⊥BC，DE⊥AB 于 E，DF⊥AC 于 F， BE＝CF．
（1）求证：AD 是∠BAC 的平分线；
（2）如果 AB＝8，AC＝6，求 AE 的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成推理填空：如图在△ABC中，已知∠1+∠2=180°，∠3=∠B，试说明∠AED=∠C．
解：∵∠1+∠2=180°（已知），
∠1+∠EFD=180°（邻补角定义），
∴∠2=∠EFD（ ）
∴AB∥EF（内错角相等，两直线平行）
∴∠ADE=∠3（ ）
∵∠3=∠B（已知）
∴∠ADE=∠B（ ）
∴ （同位角相等，两直线平行）
∴∠AED=∠C（两直线平行，同位角相等）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
（1）在这项调查中，共调查了多少名学生？
（2）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；
（3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】“马航事件”的发生引起了我国政府的高度重视，迅速派出了舰船和飞机到相关海域进行搜寻．如图，在一次空中搜寻中，水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体（该物体视为静止）．为了便于观察，飞机继续向前飞行了800米到达B点，此时测得点F在点B俯角为45°的方向上，请你计算当飞机飞临F点的正上方点C时（点A、B、C在同一直线上），竖直高度CF约为多少米？（结果保留整数，参考数值：
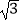≈1.7）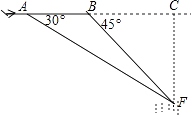
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
中，
，D，E，F分别为AB，BC，CA上的点，且
，
．（1）求证：
≌
；（2）若
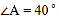，求
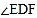的度数．
相关试题
