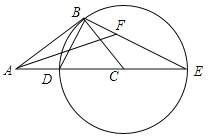
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
(1)求证:△ABD∽△AEB;
(2)当![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)要证明△ABD∽△AEB,已经有一组对应角是公共角,只需要再找出另一组对应角相等即可.
(2)由于AB:BC=4:3,可设AB=4,BC=3,求出AC的值,再利用(1)中结论可得AB2=ADAE,进而求出AE的值,所以tanE=![]() ;
;
(3)设设AB=4x,BC=3x,由于已知AF的值,构造直角三角形后利用勾股定理列方程求出x的值,即可知道半径3x的值.
试题解析:(1)∵∠ABC=90°,∴∠ABD=90°﹣∠DBC,由题意知:DE是直径,∴∠DBE=90°,∴∠E=90°﹣∠BDE,∵BC=CD,∴∠DBC=∠BDE,∴∠ABD=∠E,∵∠A=∠A,∴△ABD∽△AEB;
(2)∵AB:BC=4:3,∴设AB=4,BC=3,∴AC=![]() =5,∵BC=CD=3,∴AD=AC﹣CD=5﹣3=2,由(1)可知:△ABD∽△AEB,∴
=5,∵BC=CD=3,∴AD=AC﹣CD=5﹣3=2,由(1)可知:△ABD∽△AEB,∴![]() ,∴
,∴![]() =ADAE,∴
=ADAE,∴![]() =2AE,∴AE=8,在Rt△DBE中
=2AE,∴AE=8,在Rt△DBE中
tanE=![]() =
=![]() =
=![]() ;
;
(3)过点F作FM⊥AE于点M,∵AB:BC=4:3,∴设AB=4x,BC=3x,∴由(2)可知;AE=8x,AD=2x,∴DE=AE﹣AD=6x,∵AF平分∠BAC,∴![]() ,∴
,∴![]() ,∵tanE=
,∵tanE=![]() ,∴cosE=
,∴cosE=![]() ,sinE=
,sinE=![]() ,∴
,∴![]() ,∴BE=
,∴BE=![]() ,∴EF=
,∴EF=![]() BE=
BE=![]() ,∴sinE=
,∴sinE=![]() =
=![]() ,∴MF=
,∴MF=![]() ,∵tanE=
,∵tanE=![]() ,∴ME=2MF=
,∴ME=2MF=![]() ,∴AM=AE﹣ME=
,∴AM=AE﹣ME=![]() ,∵
,∵![]() ,∴
,∴![]() ,∴x=
,∴x=![]() ,∴⊙C的半径为:3x=
,∴⊙C的半径为:3x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】只用一种多边形不能镶嵌整个平面的是( )
A.正三角形B.正四边形C.正五边形D.正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间上映的第一部中国科幻电影《流浪地球》,斩获约4 670 000 000元票房,将4 670 000 000用科学记数法表示是( )
A. 4.67×1010B. 0.467×1010C. 0.467×109D. 4.67×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形三个内角度数的比为2:3:5,那么这个三角形是( )
A.直角三角形B.锐角三角形C.钝角三角形D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段
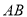 、
、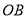 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程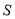 (米)与所用时间
(米)与所用时间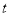 (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):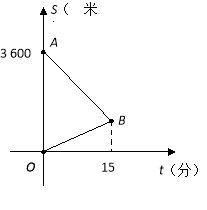
【1】求点
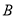 的坐标和
的坐标和 所在直线的函数关系式
所在直线的函数关系式【2】小明能否在比赛开始前到达体育馆
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,D,C,F在同一直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需添加一个条件是( )
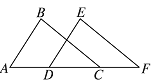
A. ∠BCA=∠F B. ∠B=∠E C. BC∥EF D. ∠A=∠EDF
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是91个,则每个支干长出的小分支数目为
相关试题

