【题目】如图:已知ABCD中,以AB为斜边在ABCD内作等腰直角△ABE,且AE=AD,连接DE,过E作EF⊥DE交AB于F交DC于G,且∠AEF=15°
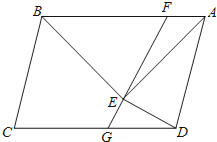
(1)若EF=![]() ,求AB的长.
,求AB的长.
(2)求证:2GE+EF=AB.
参考答案:
【答案】(1)AB=3;(2)见解析
【解析】
试题分析:(1)作EH⊥AB,交AB于H,根据等腰直角三角形的性质得到∠EAB=∠EBA=45°,EA=EB,于是得到EH=HB=AH=![]() AB,于是得到∠EFH=∠EAB+∠AEF=60°,求得∠FEH=30°,根据直角三角形的性质即可得到结论;
AB,于是得到∠EFH=∠EAB+∠AEF=60°,求得∠FEH=30°,根据直角三角形的性质即可得到结论;
(2)连接EC,根据三角形的内角和得到∠DEA=∠EDA=75°,于是得到∠EAD=30°,求出∠DAB=∠DCB=75°,∠CBA=∠CDA=105°,由于∠ABE=45°,得到∠CBE=60°,推出△BCE是等边三角形,求出∠DCE=15°,CE=BE=AE,推出DG=2GE,证得△AEF≌△ECG,根据全等三角形的性质得到GC=FE,即可得到结论.
解:(1)作EH⊥AB,交AB于H,
∵△ABE是等腰直角三角形,
∴∠EAB=∠EBA=45°,EA=EB,
∴EH=HB=AH=![]() AB,
AB,
∴∠EFH=∠EAB+∠AEF=60°,
∴∠FEH=30°,
∴FH=![]() EF=
EF=![]() EH=
EH=![]() ,
,
∴AB=3,
(2)连接EC,
∵∠AEF=15°,EF⊥DE,AE=AD,
∴∠DEA=∠EDA=75°,
∴∠EAD=30°,
∵∠BAE=45°,
∴∠DAB=∠DCB=75°,∠CBA=∠CDA=105°,
∵∠ABE=45°,
∴∠CBE=60°,
∵AD=BE=BC,
∴△BCE是等边三角形,
∴∠DCE=15°,CE=BE=AE,
∵∠GED=90°,∠GDC=30°,∠DGE=60°,
∴DG=2GE,
∵∠EGC=105°=∠AFE,CE=EF,∠DCE=15°=∠AEF,
在△AEF与△ECG中, ,
,
∴△AEF≌△ECG,
∴GC=FE,
∴AB=DC=DG+GC=2GE+CG=2GE+EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜店第一次用800元购进某种蔬菜,由于销售状况良好,该店又用1400元第二次购进该品种蔬菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有3%的损耗,第二次购进的蔬菜有5%的损耗,若该蔬菜店售完这些蔬菜获利不低于1244元,则该蔬菜每千克售价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.
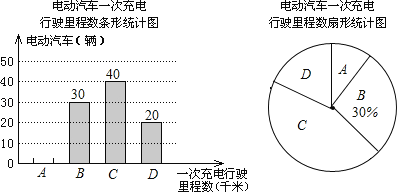
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字3、4、5,现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.如果和为奇数,则小明胜;和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为8的概率;
(2)你认为这个游戏对双方公平吗?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段为边,能组成三角形的是( )
A. 2cm、2cm、4cm B. 8cm、6cm、3cm
C. 2cm、6cm、3cm D. 11cm、4cm、6cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】x是(﹣3)2的平方根,y是64的立方根,则x+y=( )
A. 3 B. 7 C. 3,7 D. 1,7
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC的三边长a,b,c满足a2+b2+c2+50=6a+8b+10c,则△ABC的形状是什么?
相关试题

