【题目】如图，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．

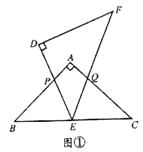
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；

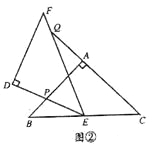
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP= ，CQ= 时，P、Q两点间的距离 (用含的代数式表示)．

参考答案：

【答案】（1）由△ABC是等腰直角三角形，易得∠B=∠C=45°，AB=AC，又由AP=AQ，E是BC的中点，利用SAS，可证得△BPE≌△CQE；

（2）由△ABC和△DEF是两个全等的等腰直角三角形，易得∠B=∠C=∠DEF=45°，然后利用三角形的外角的性质，即可得∠BEP=∠EQC，则可证得△BPE∽△CEQ；PQ=a

【解析】试题分析：（1）由△ABC是等腰直角三角形，易得∠B=∠C=45°，AB=AC，又由AP=AQ，E是BC的中点，利用SAS，可证得：△BPE≌△CQE；

（2）由△ABC和△DEF是两个全等的等腰直角三角形，易得∠B=∠C=∠DEF=45°，然后利用三角形的外角的性质，即可得∠BEP=∠EQC，则可证得：△BPE∽△CEQ；根据相似三角形的对应边成比例，即可求得BE的长，即可得BC的长，继而求得AQ与AP的长，利用勾股定理即可求得P、Q两点间的距离．

∵△ABC是等腰直角三角形，

∴∠B=∠C=45°，AB=AC，

∵AP=AQ，

∴BP=CQ，

∵E是BC的中点，

∴BE=CE，

∴△BPE≌△CQE（SAS）；

（2）连接PQ

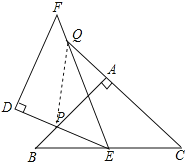
∵△ABC和△DEF是两个全等的等腰直角三角形，

∴∠B=∠C=∠DEF=45°，

∵∠BEQ=∠EQC+∠C，即∠BEP+∠DEF=∠EQC+∠C，

∴∠BEP+45°=∠EQC+45°，

∴∠BEP=∠EQC，

∴△BPE∽△CEQ，

∴，

∵BP=a，CQ=a，BE=CE，

∴，

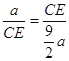∴BE=CE=，

∴BC=3，

∴AB=AC=BCsin45°=3a，

∴AQ=CQ-AC=，PA=AB-BP=2a，

关闭