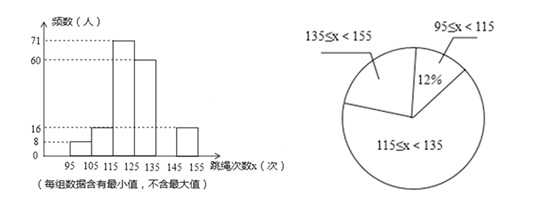
【题目】在我县开展的“阳光体育”跳绳活动中,为了了解初中学生跳绳活动的开展情况,随机抽查了全县七年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,直接写出扇形统计图中跳绳次数范围135≤x<155所在扇形的圆心角度数;
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全县8000名初中学生中有多少名学生的成绩为优秀?
(4)请你根据以上信息,对我市开展的学生跳绳活动谈谈自己的看法或建议.
参考答案:
【答案】解:(1)抽查的总人数:(8+16)÷12%=200(人)。
(2)范围是135≤x<145的人数是:200﹣8﹣16﹣71﹣60﹣16=29(人),补全频数分布直方图如下:

扇形统计图中跳绳次数范围135≤x≤155所在扇形的圆心角度数为81°。
(3)优秀的比例是:![]() ×100%=52.5%,
×100%=52.5%,
∴估计全市8000名八年级学生中有多少名学生的成绩为优秀人数是:
8000×52.5%=4200(人)。
(4)全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好。
【解析】试题分析:(1)利用95≤x<115的人数是8+16=24人,所占的比例是12%即可求解。
(2)求得范围是135≤x<145的人数,补全频数分布直方图。
跳绳次数范围135≤x≤155所在扇形的圆心角度数是:360×![]() =81°。
=81°。
(3)首先求得所占的比例,然后乘以总人数8000即可求解。
(4)根据实际情况,提出自己的见解即可,答案不唯一。
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红随机调查了50名九年级同学某次知识问卷的得分情况,结果如下表:
问卷得分(单位:分)
65
70
75
80
85
人数(单位:人)
1
15
15
16
3
则这50名同学问卷得分的众数和中位数分别是 ( )
A. 16,75 B. 80,75 C. 75,80 D. 16,15
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④


A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
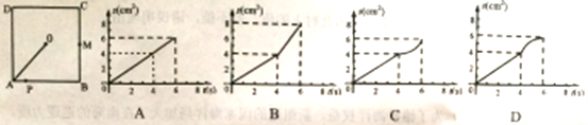
查看答案和解析>>【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图像可以是( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
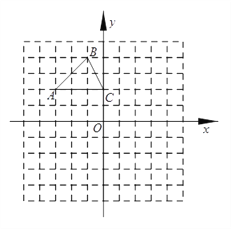
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
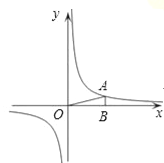
查看答案和解析>>【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
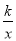 (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为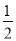 .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=
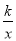 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;(3)过原点O的直线l与反比例函数y=
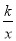 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,三角形ABC的顶点都在网格点上。
(1)平移三角形ABC,使点C与坐标原点O是对应点,请画出平移后的三角形A′B′C′;
(2)写出A、B两点的对应点A′、B′的坐标;
(3)求出三角形ABC的面积。

相关试题

